5.1.4 Beschreibung der dichtesten Packungen anhand von Koordinationspolyedern
Wie bereits des öfteren erwähnt, lassen sich die Kugeln in den dichtesten Kugelpackungen zu Gruppierungen von Tetraedern und Oktaedern, von Polyedern zusammenfassen (vgl. Abb. 5.11). Also muß es möglich sein, die dichtesten Kugelpackungen symbolisch durch Tetraeder und Oktaeder zu beschreiben, so daß sie in der Gesamtbetrachtung übersichtlicher werden. Die Polyeder ergeben gleichzeitig eine klare Darstellung der Hohlräume in den Kugelpackungen. Ein einziger Oktaeder, den man von der Dreiecksfläche ausgehend von oben betrachtet, liefert bereits Informationen, wie zwei Kugelschichten in Dreiecksmaschen übereinanderliegen. Anhand von vielen Oktaedern, die auf einer Fläche aneinandergereiht sind, können wir zwei Kugelschichten symbolisch darstellen (vgl. (1) und (2) in Abb. 5.12).
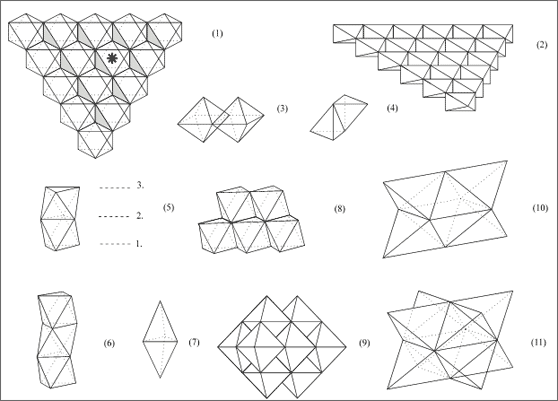
Abbildung 5.12: Symbolische Darstellung dichtester Kugelpackungen durch Tetraeder und Oktaeder
Das gestrichelte Dreiecksmuster (1) symbolisiert die untere, die durchgezogenen Dreiecke deuten die obere Schicht an, wobei die Sechsecke jeweils die Oktaeder und die Dreiecke mit Mittelpunkt die Tetraeder anzeigen. Die gestrichelten Dreiecke weisen auf Tetraeder mit der Spitze nach oben hin, die durchgezogenen auf solche mit der Spitze nach unten. Jeder Punkt ist somit gleichzeitig Eckpunkt von Oktaedernund von Tetraedern, in der Flä-chendarstellung (1) stoßen jeweils 3 Oktaeder und 3 Tetraeder in einem Punkt zusammen. Stellen wir uns beispielsweise den Oktaeder (*) räumlich vor, dann ist zu sehen, daß jede Dreiecksfläche des Oktaeders, außer unten und oben, von einem Tetraederbegrenzt wird.
Die Dreiecksflächen der oberen Schicht können wir als eine regelmäßig abwechselnde Folge von Oktaeder- und Tetraederflächen beschreiben, die Tetraeder weisen jeweils mit der Spitze nach unten. Es sei besonders betont, daß in einer Schicht sowohl alle Oktaeder als auch alle Tetraeder untereinander nur über die gemeinsame Kante miteinander verknüpft sind (vgl. (3) und (4) in Abb. 5.12): Kein Oktaeder teilt mit einem anderen eine gemeinsame Fläche und ebensowenig ein Tetraeder mit einem anderen.
Der räumliche Weiterbau der Oktaederschicht kann durch weiteres Aufsetzen einer Oktaederschicht erfolgen. Wie (5) in Abbildung 5.12 zeigt, entspricht dies aber nur dem Weiterbau mit einer Kugelschicht, denn die Deckschicht des ersten Oktaeders und die Grundfläche des zweiten Oktaeders gehören zu ein und derselben Kugelschicht.
Wenn wir bedenken, daß der Oktaeder auf einer Dreiecksfläche aufliegt, ergeben sich beim Weiterbau sofort wieder unsere zwei Möglichkeiten, dichteste Kugelpackungen zu herzustellen: Es handelt sich nämlich um die entscheidende dritte Kugelschicht. Wir können entweder Oktaeder auf Oktaeder und damit Tetraeder auf Tetraeder setzen oder alle Oktaeder auf die Tetraeder und umgekehrt.
Das Schichten von Oktaeder auf Oktaeder (6) entspricht der hexagonal dichtesten Kugelpackung, man sieht, daß die erste mit der dritten Schicht identisch ist und daß man von oben nach unten durch den ganzen "Oktaederturm" hindurchschauen kann. Die Mittelpunkte der Oktaeder liegen hier alle senkrecht übereinander, die Schichtung "Oktaeder auf Oktaeder" (6) bzw. "Tetraeder auf Tetraeder" (7) beschreibt die hexagonal dichteste Ku-gelpackung.
In der kubisch dichtesten Kugelpackung grenzt beim Aufeinanderschichten immer eine Tetraederfläche an eine Oktaederfläche (8). Ein Oktaeder ist demnach von acht Tetraedern begrenzt und ein Tetraeder von vier Oktaedern. Alle Oktaeder miteinander und alle Tetraeder untereinander sind nur über die Kanten verknüpft. In dieser Bauweise ist tatsächlich erst der 4. Oktaeder wieder mit dem 1. Oktaeder deckungsgleich und zeigt die Schichtenfolge ABCABC von Dreiecksmustern an.
Wenn wir die Oktaeder auf die Spitze stellen und Kante an Kante bauen, entspricht dies der Kugelbauweise 1-2-1-2 im Quadratmaschenmuster, dabei ergeben sich zwangsläufig die Tetraeder zwischen den Oktaedern (vgl. (9) in Abb. 5.12). Ein Oktaeder mit acht auf den Flächen aufgesetzten Tetraedern stellt symbolisch den kubisch-flächenzentrierten Würfel dar (vgl. (10) und (11) in Abb. 5.12). Die acht Tetraederspitzen entsprechen den Würfelecken.
![]()


