5.1.3 Hohlräume und Packungsdichte
Im letzten Abschnitt haben wir gesehen, daß selbst bei dichtester Packung von Kugeln notgedrungen immer Lücken bleiben. Diese Lücken sind unterschiedlich groß und keineswegs so klein, wie man ursprünglich vermuten möchte. Je mehr Kugeln zusammen eine Lücke ergeben, desto größer ist sie. Das können wir bereits in der Ebene sehr gut verfolgen (vgl. Abb. 5.10): Drei sich berührende Kugeln erzeugen die kleinste Lücke (1), vier Kugeln eine sichtbar größere (2) und sechs Kugeln lassen zwischen sich soviel Platz, daß wir noch eine gleichgroße Kugel hineinsetzen könnten (3).
Wir erweitern die Fragestellung auf räumliche Lücken, indem wir die Flächenlücken schließen. Bei der Dreierlücke genügt es, wenn wir eine Kugel von oben oder unten in die Mulde setzen, wir erhalten eine Lücke in Form des Tetraeders (4).
Die ebene Viererlücke im Quadratmuster kann auf zweierlei Weise zu einer räumlichen Lücke erweitert werden. Zunächst soll oben und unten je eine Kugel in die Lücke einrasten: Es ergibt sich um die Lücke herum die Kugelformation eines Oktaeders (5). Andererseits können wir auf die quadratische Lücke die gleiche ebene Viererlücke als Quadrat direkt schichtengleich daraufsetzen, die Kugelanordnung ist dann durch einen einfachen Würfel beschreibbar (6).
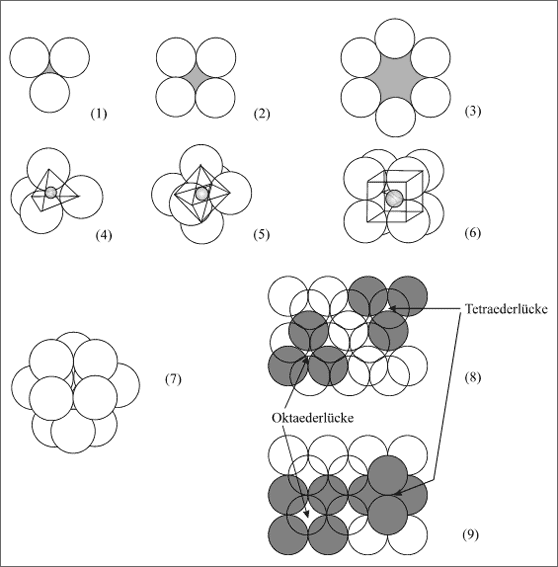
Abbildung 5.10: Mögliche Hohlräume in ebenen und räumlichen Kugelanordnungen
Die Sechsergruppierung (3) ist von einer Kugel nicht mehr abdeckbar, sondern nur von drei Kugeln. Tun wir das auf beiden Seiten, dann erhalten wir den sogenannten Kubooktaeder, in den eine Kugel derselben Größe hineinpaßt (7). Diese 12er-Anordnung ist uns aus dichtesten Kugelpackungen bereits bekannt: Sie zeigt die Koordinationszahl 12. Die Lücken in den Kugelformationen -Tetraeder-Oktaeder - Würfel-Kubooktaeder- nehmen in ihrer Größe in der angegebenen Reihenfolge zu. Das läßt sich mit Modellkugeln sehr anschaulich darstellen und spielt eine entscheidende Rolle, wenn wir später diese Lücken mit kleineren Kugeln besetzen wollen.
Für Informationszwecke werden diese Lücken danach benannt, welchen Raumkörper die Mittelpunkte der Kugeln um die Lücke herum aufbauen:
Tetraederlücke mit der Koordinationszahl 4,
Oktaederlücke mit der Koordinationszahl 6,
Würfellücke mit der Koordinationszahl 8,
Kubooktaederlücke mit der Koordinationszahl 12.
Gleichzeitig sind die Bezeichnungen "tetraedrische Lücke" für die Tetraederlücke und "oktaedrische Lücke" für die Oktaederlücke in Gebrauch. Sprachlich ist das nicht exakt, weil ja nicht die Form der Lücke gemeint ist, sondern die Formation der sie umgebenden Kugeln. Wir werden deshalb die Bezeichnungen Tetraeder- und Oktaederlücke bevorzugen.
Nun wollen wir uns die Lücken in den dichtesten Kugelpackungen näher ansehen. Diese sind gut anschaulich zu machen, auch wenn nur zwei Schichten entweder in Dreiecksmaschen oder in Quadratmaschen gestapelt sind (vgl. (8) und (9) in Abb. 5.10).
In der Dreiecksmusterschichtung (8) sind nur zwei unterschiedliche lückenbildende Kugelformationen anzutreffen: die Anordnung des Tetraeders und die des Oktaeders. Bei zusätzlicher Stapelung ändert sich an den Lücken nichts, es bleiben immer die gleichen Sorten von Hohlräumen, größere Oktaeder- und kleinere Tetraederlücken. Die hexagonal und kubisch dichteste Kugelpackung unterscheiden sich demnach nicht durch die Art der Lücken, sondern durch deren Lage.
Das gleiche Ergebnis erhalten wir bei der Betrachtung der Stapelung von Quadratmaschenschichten (9). Es tauchen immer wieder die kreuzweise übereinandergelegten Kugelpaare des Tetraeders und das beiderseits bedeckte Quadrat des Oktaeders auf (vgl. Schraffuren in Abb. 5.10).
Die Größe und Anzahl der Hohlräume zwischen den Kugeln ist ein Kennzeichen dafür, wie dicht die Kugeln zusammengepackt sind. Je mehr Kugeln bestimmter Größe in einem vorgegebenen Raum untergebracht werden können, desto kleiner müssen demzufolge die Lücken sein, umso größer ist die "Kugeldichte".
Das können wir uns übersichtlich in der Fläche an den Figuren (1) - (3) in Abbildung 5.11 verdeutlichen. Die in die Kugelanordnungen eingezeichneten Flächen sind fast gleichgroß, die Anzahl der auf den Flächen liegenden Kugeln ist aber verschieden. Wenn wir berücksichtigen, daß die Flächen einige Kugeln in Halb- oder Viertelkugeln zerschneiden, ergeben sich durch einfaches Abzählen die Ergebnisse in Tabelle 5.2.
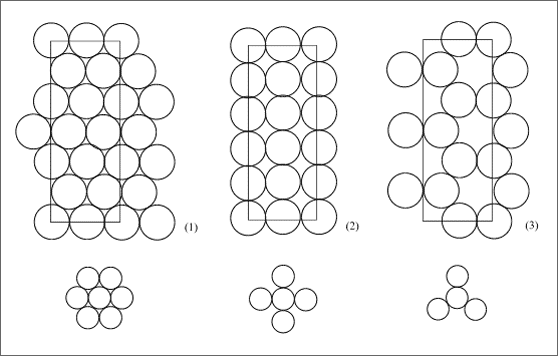
Abbildung 5.11: Verschiedene Packungsdichten gleich großer Kugeln in der Ebene
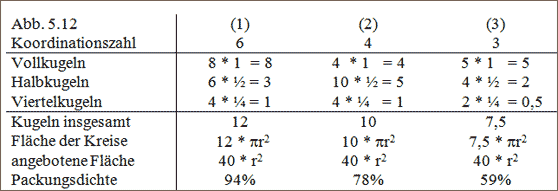
Tabelle 5.2: Berechnung verschiedener Packungsdichten
Für die Größe der zur Verfügung stehenden Fläche, gilt: 4r*10r = 40*r2. Es ist zu
erkennen, daß diese Fläche je nach der Art der Packung von immer weniger Kugeln gefüllt wird. Bezeichnet man das Verhältnis des Raumbedarfs der Kugeln zur angebotenen Fläche als Packungsdichte, so ersieht man aus Tabelle 5.2, daß die Packungsdichte mit zunehmender Koordinationszahl größer wird. Dieser Satz gilt nicht nur für die Fläche, sondern auch für den Raum. Die maximale Packungsdichte in dichtesten Kugelpackungen mit der Koordinationszahl 12 beträgt 74 %, in Kugelpackungen der Koordinationszahl 6 nur noch 52 %, in solchen der Koordinationszahl 4 lediglich 34 %.
Nicht nur die theoretisch ermittelte Packungsdichte ändert sich in angegebener Weise, sondern auch die experimentell zu messende Dichte der Substanzen. Wenn es gelingt, bei gleicher Teilchensorte die Koordinationszahl und damit die Packungsdichte zu erhöhen, dann erhöht sich zwangsläufig die Dichte der Substanz. Zum Beispiel zeigt Zinn mit der Koordinationszahl 4 eine kleinere Dichte als Zinn der Koordinationszahl 6, Eisen mit der Koordinationszahl 8 eine kleinere Dichte als Eisen mit der Koordinationszahl 12. Wenn umgekehrt Wasser eine größere Dichte besitzt als Eis, dann muß in flüssigem Wasser eine größere Koordinationszahl festzustellen sein als in festem Wasser.
![]()


