5.1.5 Die Elementarzelle als Gitterausschnitt
Bestimmte Ausschnitte aus Gittern oder Kugelpackungen werden als Elementarzelle bezeichnet. Als Beispiel mag ein einfaches Würfelgitter zugrunde gelegt werden (Vgl. (1) in Abb. 5.13). Zunächst wird mit Modellkugeln der Elementarwürfel dieses Würfelgitters mit der Koordinationszahl 6 gebaut: offensichtlich benötigen wir dazu 8 Kugeln und 12 Drähte für die Kanten (2).
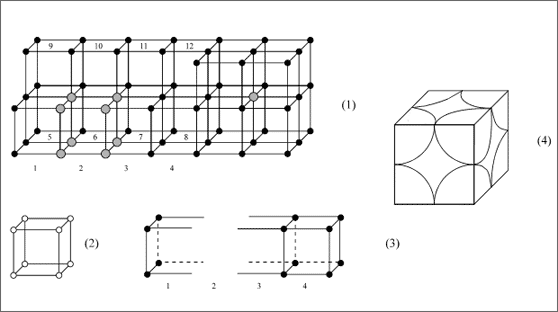
Abbildung 5.13: Einfaches Würfelgitter und Elementarzelle
Nun nehmen wir gedanklich einen solchen Elementarwürfel aus dem Würfelgitter heraus. Die untere vordere Würfelreihe zählt vier Elementarwürfel, auf den ersten Blick enthält jeder Würfel für sich die gesamte Bauinformation. Nun trennen wir den Würfel 2 heraus. Schematisch bleibt dann von der vorderen Würfelreihe nur das Skelett (3) übrig, die Würfel 1 und 3 sind zerstört, weil die halbe Anzahl der Kugeln für den Elementarwürfel (2) herausgenommen worden ist.
Damit tragen Würfel 1 und 3 die Bauinformation nicht mehr. Das gilt ebenfalls für die Würfel 5, 6, 7, 9, 10, 11 - letztlich für alle angrenzenden Würfel. Dieser Fehler ist nur vermeidbar, wenn wir die Kugeln für bestimmte Beschreibungszwecke zerschneiden. Im Inneren des Würfelgitters ist jede Kugel an acht Würfeln beteiligt, an vier Würfeln der unteren und an vier Würfeln der darüber liegenden Schicht. Beim exakten Herausschneiden eines Würfels bleibt also an jeder Ecke nur 1/8 der Kugel übrig. Auf diesem Wege gelangt man von einem Elementarwürfel (2) mit vollen Kugeln zur Elementarzelle (4) mit Achtelkugeln. Sie enthält insgesamt nur 8 x 1/8 = 1 Kugel.
Die richtig geschnittenen Modelle mit Achtelkugeln sind sehr schwer zu bauen und ungünstig zu zeichnen. Daher werden meistens ganze Kugeln für Elementarzellen gezeichnet, das richtige Schneiden der Kugeln muß der Betrachter in der Vorstellung selbst bewerkstelligen.
Setzen wir nun in jedes Raumzentrum aller Elementarwürfel des Wirtsgitters (vgl. (1) der Abb. 5.13) je eine weitere Kugel, dann erhalten wir eine sehr häufig vorkommende Kugelanordnung: das kubisch raumzentrierte Gitter oder kubisch innenzentrierte Gitter. Elementarwürfel und Elementarzelle des kubisch raumzentrierten Gitters zeigen (1) und (2) in Abbildung 5.14. Die Elementarzelle enthält demnach 8 x 1/8 Kugeln an den Ecken und die Vollkugel im Raumzentrum, also insgesamt 2 Kugeln.
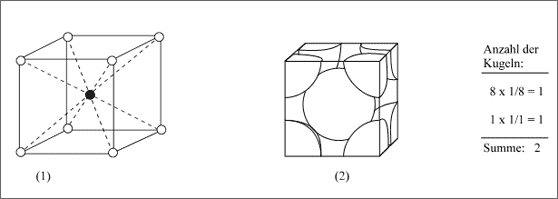
Abbildung 5.14: Kubisch raumzentriertes Gitter und Elementarzelle
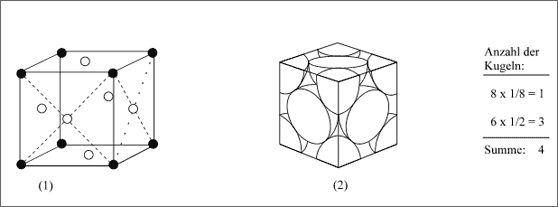
Abbildung 5.15: Kubisch flächenzentriertes Gitter und Elementarzelle
Betrachten wir den Elementarwürfel eines kubisch flächenzentrierten Gitters und schneiden gedanklich die Elementarzelle heraus (vgl. (1) und (2) der Abb. 5.15): Sie enthält 8 x 1/8 Kugeln an den Ecken und 6 x 1/2 Kugeln auf den Flächen.
Entsprechende Überlegungen an hexagonalen Elementarzellen führen zu Schnittmodellen wie beispielsweise dem Ausschnitt aus der hexagonal dichtesten Kugelpackung (vgl. (1) und (2) in Abb. 5.16). Eine Eckkugel zählt hier 1/6, denn sie muß drei Zellen des unteren Stockwerkes und drei Zellen des oberen Stockwerkes bedienen. Die Kugel im Mittelpunkt eines jeden Hexagons wird halbiert, die drei Innenkugeln zählen ganz.
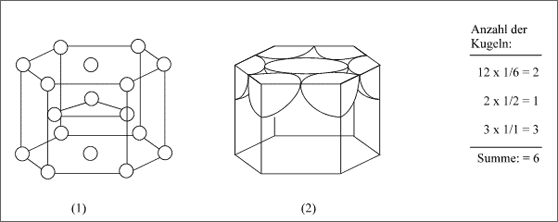
Abbildung 5.16: Üblicher Gitterausschnitt aus der hexagonal dichtesten Kugelpackung
Abbildung 5.17: Anzahl von Oktaeder- und Tetraederlücken in dichtesten Kugelpackungen
![]()


