5.2.4.2 Memorymetalle: Form-Gedächtnis-Effekt
Es gibt Metallegierungen, die bei Verformung ein eigenartiges Verhalten zeigen. Bringt man sie bei höherer Temperatur in eine bestimmte Form, beispielsweise in Stabform, und kühlt ab, so kann man nach außen nichts besonderes erkennen. Auch wenn man den Stab biegt, unterscheidet er sich äußerlich nicht vom normalen Verhalten. Wenn man den gebogenen Stab jedoch auf höhere Temperatur bringt, dann biegt er sich wie von Geisterhand wieder in die ursprüngliche Stabform zurück. Der Stab verhält sich so, als ob er ein "Erinnerungsvermögen" an seine ursprüngliche Gestalt bei höherer Temperatur hätte. Deshalb werden diese Legierungen auch Memory-Metalle genannt.
Dieser Effekt beruht auf einem Wechsel der Kristallstruktur bei genau zugeordneten Temperaturen, ähnlich dem Wechsel von α-Eisen zu γ-Eisen. Eine der bekanntesten Legierungen mit Memory-Eigenschaften besteht zu 50 Atom% aus Nickel und zu 50 Atom% aus Titan. Sie wird mit dem Symbol NiTi angegeben und Nitinol genannt. Es soll uns als Modellsubstanz für den Mechanismus des Form-Gedächtnis-Effektes dienen.
Nickel-Titan-Modifikationen. Nickel ist nur als kubisch dichteste Struktur bekannt, Titan bei Raumtemperatur als hexagonal dichteste Packung. Wenn man im Nickelgitter die Hälfte der Ni-Atome durch Ti-Atome ersetzt, lassen bereits - wie im diskutierten System Kupfer/Zink - die Ti-Atome den Bau des kubisch flächenzentrierten Gitters nicht mehr zu, allerdings die Ni-Atome auch nicht die Bauweise der hexagonal dichtesten Kugelpackung. Der Kompromiß ist - analog wie bei dem System Cu/Zn - ein kubisch innenzentriertes Gitter (vgl. (a) in Abb. 5.60).
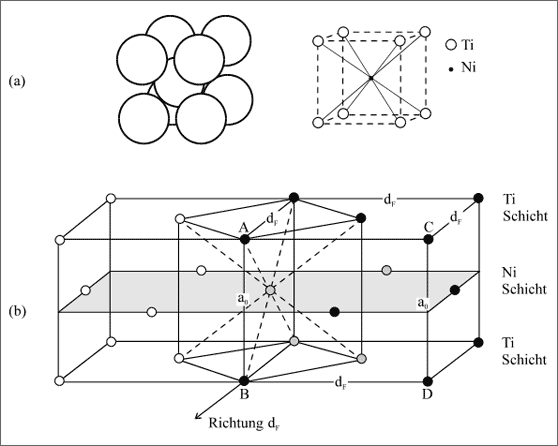
Abbildung 5.60: Strukturmodelle für die Memorylegierung Nitinol
Bei hoher Temperatur sind die Atome statistisch verteilt, bei Raumtemperatur ordnen sich die Ni- und Ti-Atome, sodaß ein Ti-Atom immer von 8 Ni-Atomen und ein Ni-Atom immer von 8 Ti-Atomen umgeben ist (vgl. (a) in Abb. 5.60). Wir kennen diese Struktur vom α-Eisen und von der Eisen-Titan-Legierung FeTi, später wird sie uns bei den Ionensubstanzen als Cäsiumchlorid CsCl wieder begegnen.
Die geordnete Struktur wird besonders gut deutlich, wenn wir nicht den raumzentrierten Würfel, sondern die anders ausgeschnittene tetragonal flächenzentrierte Zelle betrachten (vgl. (b) in Abb. 5.60). Dem innenzentrierten Würfel ordnen wir im Zentrum das kleinere Ni-Atom zu, das von 8 Ti-Atomen berührt wird. Die Kantenlänge des Würfels soll a0 betragen. Sie ist länger als der Durchmesser eines Ti-Atoms, sodaß sich keine Ti-Atome berühren.
Schneidet man den innenzentrierten Würfel senkrecht zur Flächendiagonalen dF, dann erhält man eine rechteckige Fläche mit Ti-Atomen an deren Ecken und einem Ni-Atom im Flächenzentrum. Vier dieser Flächen bilden die Seitenflächen der tetragonalen Zelle, Deckfläche und Grundfläche sind Quadrate mit der Seitenkante dF. Wir könnten natürlich auch die gesamte Konstruktion als Lagen von kleinen Quadratmaschen beschreiben, die abwechselnd aus Ti-Atomen und Ni-Atomen bestehen. Insofern sind die Flächenzentren der flächenzentrierten, tetragonalen Zelle auf den Seiten mit Ni-Atomen besetzt, auf den quadratischen Deckflächen jedoch mit Ti-Atomen.
Die Zuordnung von Ti- und Ni-Atomen in der Fläche ist besonders gut anhand der Rechtecksschichten zu sehen: solch eine Schicht ist in Abbildung 5.61 (a) herausgestellt. Das Größenverhältnis von Ni- zu Ti-Atomen ist 0,86, man erkennt, daß sich die Ti-Atome nicht berühren: Bindungen bestehen nur zwischen Ti- und Ni-Atomen. In dieser Schicht sind fünf Lücken gekennzeichnet: sie zeigen die Plätze, an welchen vier Ti-Atome und ein Ni-Atom der nächsten Schicht einrasten (vgl. (b) in Abb. 5.61). Dabei berührt ein Ti-Atom immer nur zwei Ni-Atome der darüberliegenden Schicht und ein Ni-Atom nur zwei Ti-Atome, die Schichtenfolge ist 1-2-1-2.
Im Gegensatz zur geordneten Struktur sieht eine entsprechende Fläche der ungeordneten Struktur aus, wie Abbildung 5.61 (c) es zeigt. In einer solchen Fläche sind auch immer mehrere Ti-Atome untereinander verknüpft und ebenso mehrere Ni-Atome. Die unterschiedlichen Durchmesser der beiden Teilchensorten bewirken, daß die Fläche nicht mehr exakt anhand von Rechtecken zu beschreiben ist. Die kleinen Abweichungen heben sich aber infolge der großen Anzahl von Teilchen gegenseitig auf.
Besonders zu beachten ist nun der Mechanismus, nach dem sich solch eine ungeordnete Struktur in eine geordnete umwandeln kann. Dabei ist zu berücksichtigen, daß sich die Teilchen bei hoher Temperatur alle unregelmäßig schwingend in Bewegung befinden. Infolge dieser Bewegung können sie tatsächlich ab und zu Plätze tauschen, sie wandern ganz langsam innerhalb des Kristalls umher: Diese Erscheinung wird als Diffusion bezeichnet.
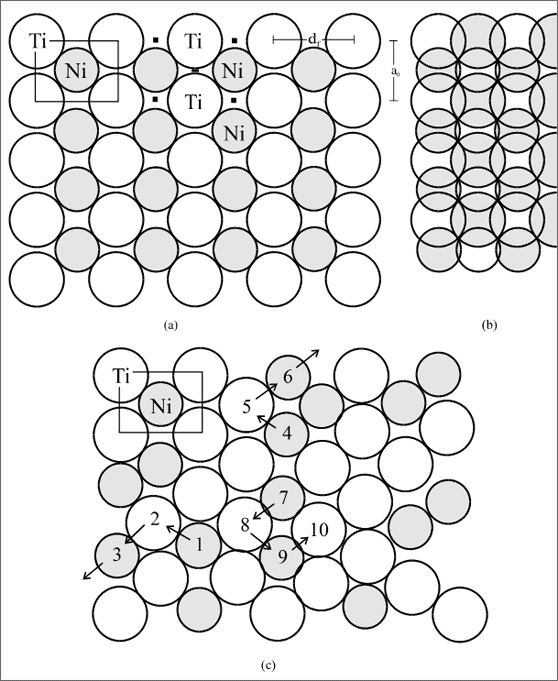
Abbildung 5.61: Geordnete und ungeordnete NiTi-Strukturen
Soll sich aus einer ungeordneten Struktur die geordnete Struktur bilden (vgl. (a) und (c) in Abb. 5.61), dann ist dies nur durch Diffusion möglich. Beispielsweise muß das Teilchen 1 auf den Platz des Teilchens 2, Teilchen 2 auf Platz 3, usw. Mögliche Wanderungen bis Teilchen 10 sind angedeutet, wobei zur Orientierung eine Zelle eingezeichnet ist.Wir halten die Kriterien fest, die Teilchenbewegungen als Diffusion kennzeichnen:
1. Die Bewegungen und Wege der Teilchen müssen völlig un-
regelmäßig, statistisch in alle Raumrichtungen verlaufen.
2. Die Weglänge muß mehr als einen Teilchendurchmesser
betragen.
3. Der Zeitfaktor muß berücksichtigt werden: Diffusions-
vorgänge dauern lange.
Anschließend werden wir anders geartete Teilchenbewegungen von der Diffusion abgrenzen.
Die kubisch raumzentrierte, geordnete Struktur des Nitinol NiTi ist bis zu Temperaturen von etwa 100°C beständig. Bei 50°C kann sich dieses Gitter jedoch in eine weitere Struktur umwandeln, die bei niedrigen Temperaturen stabil ist. Dabei werden ausgehend von der kubisch raumzentrierten Anordnung ganze Kugelreihen und -flächen gleichmäßig um einen relativ geringen Betrag im Gleichklang verschoben. Wie auf Kommando bewegen sich tausende und abertausende von Atomen im Kollektiv um denselben Betrag in die gleiche Richtung.
Betrachten wir Abbildung 5.62 (a). Kugeln sind zu einer Reihe im Abstand c' in Richtung c angeordnet, darüber im Abstand h1 eine gleiche Kugelreihe. Die Kugelreihen seien durch starre Achsen verknüpft. Wenn wir nun die Kugelreihe (1) festhalten und die Kugelreihe (2) in Pfeilrichtung schieben, rollen die Kugeln der Reihe (2) umso stärker in die Lücken zwischen die Kugeln der Reihe (1), je mehr wir die Kugelreihe (2) verschieben. Die maximale Verschiebung, ohne den ursprünglichen Abstand c' zu verändern, zeigt (b): Die Höhe h1 hat sich zur Höhe h2 verringert und die a-Achse durch die Mittelpunkte der Kugeln ist zur c-Achse schiefwinklig.
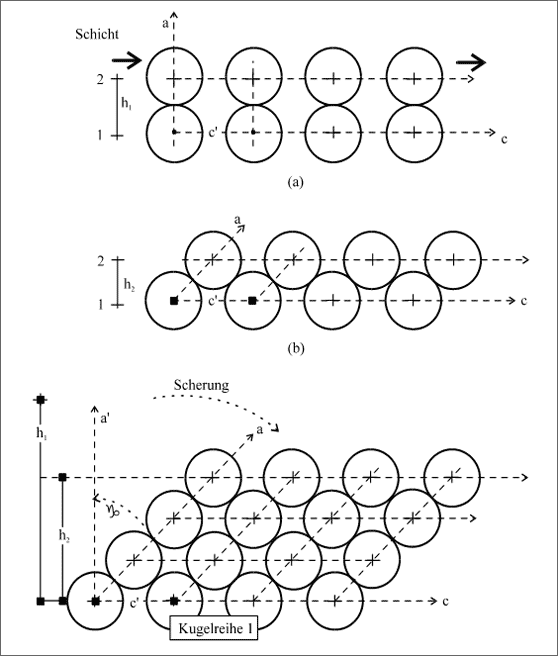
Abbildung 5.62: Strukturänderung durch Scherung
Den gleichen Effekt zeigt Abbildung 5.62 (c): Ausgehend von der zur c-Achse senkrechten a-Achse wird durch kollektives Verschieben der Kugeln die Höhe zu h2 verringert, der Achsenwinkel verkleinert, die Rechtecksform der Zelle zum Parallelogramm geändert. Wenn wir die Kugelreihen als übereinandergeschichtete Kugelflächen betrachten, haben wir durch die gleichmäßige Verschiebung der Flächen aus einem Quader ein schiefwinkliges Prisma geformt.
Es muß jedoch nochmals betont werden, daß die Kugeln relativ zu ihren Nachbarkugeln alle die gleiche Bewegung durchführen. Die Mittelpunkte der Kugeln erzeugen ein Gitter von Parallelogrammen, das als Scherengitter bekannt ist. Insofern bezeichnet man die kollektive Bewegung dieser Art als Scherung. Sie wird anhand des Scherwinkels angegeben, der in unserem Beispiel die Änderung der a-Achse gegen die c-Achse angibt. Der Scherwinkel kann kleiner oder größer sein, die Verschiebung führt aber die Kugeln nie über einen Kugeldurchmesser relativ zur Nachbarkugel hinaus. Es ist festzuhalten, daß eine Scherung die Lage der Teilchen, entsprechend die Gitterstruktur und somit die Eigenschaften der Substanz ändert.
Solche Änderungen der Struktur durch Scherprozesse sind von den Änderungen durch Diffusion begrifflich zu trennen. Scherprozesse und ähnliche Verschiebungen werden daher als diffusionslose Kristallgitteränderungen bezeichnet. Diffusionslose Gitteränderungen sind im Gegensatz zur Diffusion durch folgende drei Kriterien gekennzeichnet:
1. Die Bewegungen und Wege der Teilchen müssen völlig
regelmäßig und gleichmäßig im Gitter verlaufen.
2. Die zurückgelegte Weglänge relativ zum Nachbarn muß
weniger als einen Teilchendurchmesser betragen.
3. Der Zeitfaktor kann nahezu unberücksichtigt bleiben:
Diffusionslose Vorgänge verlaufen infolge der kleinen
Wege blitzschnell.
Solch einem diffusionslosen Scherprozeß ist die kubisch raumzentrierte Zelle des NiTi-Gitters bei 50°C unterworfen, wenn man Wärme entzieht. Die Scherung soll wiederum besser am tetragonal flächenzentrierten Ausschnitt beschrieben werden (vgl. Abb. 5.60 und Abb. 5.63): Es ist zu erkennen, daß die Ti- und Ni-Schichten in Richtung dF ganz kleine Scherbewegungen ausführen. Obwohl die Bewegung nur sehr klein ist, ist die Wirkung für den Bau des Gitters ganz erheblich: Die Verschiebung in einer Richtung schafft bessere Lücken für das Einrasten der neuen Schichten und eine höhere durchschnittliche Koordinationszahl. Bei diesem "Einrastprozeß" werden einzelne Atome ganz leicht von ihren ursprünglichen Positionen zusätzlich zur Scherung etwas hin- und hergeschoben. Dieses ganz leichte, regelmäßige Hin- und Herschieben innerhalb der Elementarzelle wird auch mit dem englischen Ausdruck Shuffle bezeichnet.
Die Scherbewegung im kubisch raumzentrierten Gitter wird an den flächenzentrierten Schichten in Richtung der Flächendiagonalen dF genauer (vgl. Abb. 5.64). Die Seitenfläche der tetragonal flächenzentrierten Zelle soll die Höhe h1 und die Kantenlänge dF in Richtung c' besitzen. Die Ecken sind hier von Ti-Atomen, das Zentrum ist von einem Ni-Atom besetzt. An den markierten Lücken a rasten Ni-Atome der darüberliegenden Schicht ein, die markierten Lücken b geben Positionen für Ti-Atome der nächsten Schicht an.
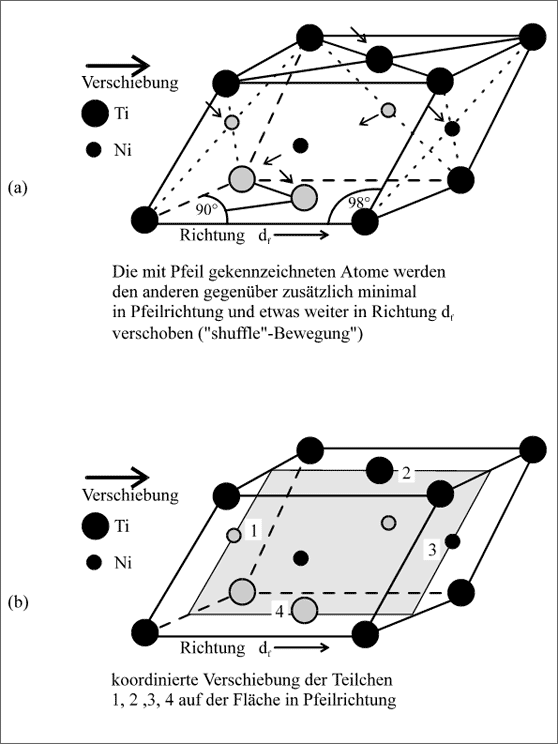
Abbildung 5.63: Modellvorstellungen für die Scherung des NiTi-Gitters und für die "Shuffle"-Bewegung der Teilchen
Wenn man eine Kraft F in angegebener Pfeilrichtung auf die oberen Ti-Atome wirken läßt, ist die Kugelreihe nicht so einfach zu verschieben, denn die Ni-Atome im Zentrum der Fläche blockieren zunächst die Bewegung in Richtung c (vgl. (a) und (b) in Abb. 5.64). Die Kugelreihe 1-2-3 wird gleichsam auf die Höhe a2 angehoben, um sie danach absinken zu lassen (c). Danach bildet das Ni-Atom nicht mehr das Zentrum der Fläche, das Rechteck ist zum Parallelogramm geworden. Die a-Achse mit einem Winkel von 97,8° gegen die c-Achse spiegelt die Scherung von 7,8° wider. Dieser Scherwinkel der NiTi-Modifikation kann bei einer Temperatur von 50°C experimentell bestätigt werden.
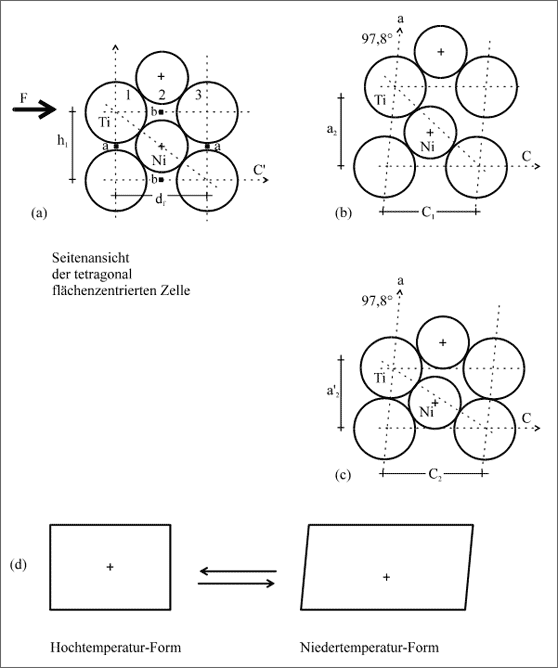
Abbildung 5.64: Betrachtungen des Schervorgangs an einer Seitenfläche der tetragonal flächenzentrierten Zelle
Mit der Scherung verbunden ist aber gleichzeitig noch eine Aufweitung des Kugelabstandes in Richtung c vom Betrag c1 auf c2 (vgl. (c) in Abb. 5.64). Dabei rutschen die Ni-Atome etwas mehr zwischen die Ti-Atome der Richtung c, bis sich die Ti-Atome berühren. Die Höhe a2' des neuen Parallelogramms ist dann kleiner als die Höhe h1 der ursprünglichen Rechtecksfläche, das Verhältnis der Seiten des Parallelogramms 1,6, der Winkel 7,8°. Diese Darstellung entspricht den experimentellen Meßdaten des NiTi-Gitters bei niederen Temperaturen.
Vergleichen wir die Kugelpositionen (siehe (a) und (c) in Abb. 5.64), so fällt auf, daß sich ein Ti-Atom vom zentralen Ni-Atom getrennt hat. Somit sind nur noch drei Ti-Atome an das Ni-Atom gebunden, dafür sind aber zwei neue Bindungen zwischen den Ti-Atomen gebildet worden - eine neue Bindung ist hinzugekommen. Die Stärke der Bindungen zwischen den Teilchen können wir an den Schmelztemperaturen der Substanzen Titan, Nickel und Nitinol abschätzen:
Ti 1672°C, Ni 1453°C, NiTi 1310°C
Demnach ist die Ti-Ti-Bindung die stärkste, die Bindung Ni-Ni etwas schwächer und die Bindung Ni-Ti am schwächsten. Insofern können wir die Strukturänderung dahingehend deuten, daß schwächere Bindungen im NiTi getrennt und dafür stärkere Bindungen gebildet werden.
Die Strukturänderungen von der Hochtemperatur zur Niedertemperaturform werden anhand der flächenzentrierten Zelle in (d) der Abbildung 5.64 zusammengefaßt und symbolisiert. Abbildung 5.65 zeigt einen größeren Ausschnitt aus der Kugelfläche der Niedertemperaturstruktur und mit schraffierten Kugeln die Anordnung von Kugeln der folgenden Schicht: Sie ist lediglich die um 180° gedrehte Grundfläche. Die dritte Schicht ist wieder identisch mit der ersten, die Schichtenfolge lautet also ABAB.

Abbildung 5.65: Anordnung und Schichtung von Ti- und Ni-Atomen ausgehend von der gescherten tetragonal flächenzentrierten Zelle
Mit der Scherung der kubisch raumzentrierten Zelle in der besprochenen Art haben sich auch die Koordinationszahlen geändert. Ausgegangen sind wir davon, daß vor der Verschiebung 8 Ti-Atome ein Ni-Atom und 8 Ni-Atome ein Ti-Atom berührend, also bindend umgeben.
Die Abbildung 5.65 läßt erkennen, daß ein Ti-Atom zwischen die Teilchen (1), (2) und (3) einrastet, es berührt also 2 Ni-Atome und 1 Ti-Atom. Innerhalb der zweiten, ebenso wie in der ersten Schicht, ist ein Ti- Atom von 3 Ni-Atomen und 2 Ti-Atomen gebunden. Nachdem die erste mit der dritten Schicht identisch ist, wird das betrachtete Ti-Atom von ebenfalls 2 Ni-Atomen und einem Ti-Atom abgedeckt.
Damit sind räumlich betrachtet an ein Ti-Atom 7 Ni-Atome und 4 Ti-Atome gebunden, also besitzt das Ti-Atom die Koordinationszahl 11. Bei dem Strukturwandel hat das Ti-Atom eine Ti-Ni-Bindung gegen 4 neue Ti-Ti-Bindungen eingetauscht.
Das Ni-Atom bindet dagegen nur Ti-Atome: zunächst etwa die beiden Teilchen (4) und (5) der unteren Schicht, in der eigenen Schicht drei und in der Deckschicht wieder zwei. Das sind räumlich gesehen insgesamt 7 Ti-Atome. Für die Ni-Atome war demnach die Verschiebung ein Negativgeschäft. Wenn wir jedoch die mittlere Koordinationszahl beider Teilchensorten aus der Koordinationszahl 11 und 7 bilden, dann erhalten wir die Koordinationszahl 9. Das ist eine höhere Koordinationszahl als 8 im Ausgangsgitter. Folglich sind in der verschobenen Struktur die Teilchen dichter gepackt, die Dichte ist größer. Das bestätigen auch die Messungen an den Nickel-Titan-Legierungen.
Austenit-Martensit-Strukturen. Der diffusionslose Strukturwandel ist in ähnlicher Weise wie beim Nitinol auch beim Eisen und Zinn bekannt. Abbildung 5.66 zeigt schematisch die Änderungen der Hochtemperatur-Struktur zur Niedertemperatur-Struktur im Vergleich mit Nitinol.
Die Hochtemperaturform wird in der Literatur auch Austenit genannt, die Niedertemperaturform Martensit. An dieser Stelle sei darauf hingewiesen, daß die Sprachregelung zur Benennung dieser und ähnlicher Substanzen verwirren kann. Das hat historische Hintergründe. Zu den ersten diffusionslosen Strukturumwandlungen, die aufgeklärt worden sind, gehören die im Zusammenhang des Stahlhärtens auftretenden Eisen-Modifikationen Kohlenstoff-Einlagerungskristalle, sie sind Austenit und Martensit genannt worden. Die spezielle Substanz Austenit, der die Struktur des γ-Eisens zuzuordnen ist, stellt die Hochtemperaturstruktur zur speziellen Substanz Martensit dar, der als Niedertemperaturstruktur die Struktur des α-Eisens zugrunde liegt.
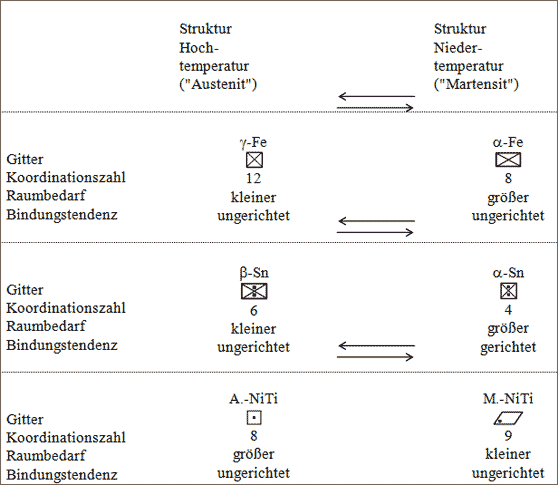
Abbildung 5.66: Änderungen der Hochtemperatur-Struktur zur Niedertemperatur-Struktur bei Eisen, Zinn und Nitinol
Nun haben sich die Ausdrücke Austenit und Martensit mit dem weiteren Auffinden von diffusionslosen Strukturwandlungen verselbständigt und verallgemeinert. Zunächst ist der Übergang vom kubisch flächenzentrierten Gitter in das kubisch raumzentrierte Gitter bei anderen Substanzen, etwa bei Nickellegierungen, allgemein als Austenit-Martensit-Umwandlung bezeichnet worden, unabhängig von der Anwesenheit des Kohlenstoffs. Im weiteren Verlauf der Erkenntnisse wurde dann allgemein bei einer diffusionslosen Strukturumwandlung die Hochtemperaturform "Austenit" und die Niedertemperaturform "Martensit" genannt, unabhängig von der Zusammensetzung und dem Kristallgitter der Substanz. Insofern wird die Hochtemperaturform von Nitinol NiTi allgemein als Austenit und die Niedertemperaturform als Martensit bezeichnet (vgl. Abb. 5.66). Der Übergang dieser Strukturen wird unter dem Begriff der martensitischen Umwandlungen zusammengefaßt. Dies ist beim Studium der Fachliteratur zu beachten.
Kristallstruktur und makroskopische Form. Eine Kristallstruktur, deren Bau im kleinsten ungestört begonnen und ständig fortgeführt wird, führt im Makroskopischen zum Einkristall. Die äußere Form hängt aber davon ab, an welchen Ecken und Enden letztlich weitergebaut wird. Beginnen wir mit einer kubisch flächenzentrierten Zelle, dann läßt sich das Männchen bauen, wie es Abbildung 5.67 (a) zeigt. Obwohl das Baumuster des flächenzentrierten Quadrats exakt eingehalten worden ist, kann die äußere makroskopische Form vielfältig verändert gewählt werden.
Wenn wir nun die Grundstruktur des flächenzentrierten Würfels diffusionslos in das kubisch raumzentrierte bzw. das tetragonale flächenzentrierte Gitter (b) umwandeln, dann muß die Figur niedriger und breiter werden: das Männchen verändert seine makroskopische Form von (a) nach (b).
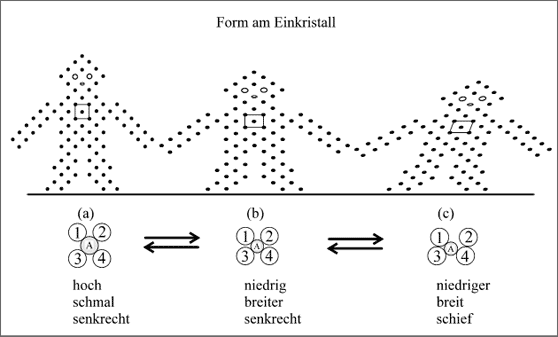
Abbildung 5.67: Schematische Modelle zu Kristallstrukturen und makroskopischen Formen (Habitus)
Wenn das Männchen aus Eisen wäre, könnten wir diese Formänderung bei 906°C, der Umwandlungstemperatur von α-Eisen (Struktur (b) ) zu γ-Eisen (Struktur (a) ), beobachten.
Bei der Zufuhr von Wärme würde das breite und niedrige Männchen (b) schmaler und höher werden, also zu (a), bei Wärmeentzug wäre es wieder breit und niedrig. Über der Umwandlungstemperatur ist γ-Eisen stabil, unter der Temperatur ist α-Eisen stabil. Würden wir die Temperatur des Männchens ständig zwischen etwa 850°C und 950°C hin und herwechseln, würde sich auch ständig die Form mit ändern. Da es sich immer um die gleiche, reproduzierbare Formänderung handelt, können wir von der makroskopischen Betrachtung ausgehend annehmen, daß sich die Hochtemperaturform an die Niedertemperaturform "erinnert" und umgekehrt. Das "Erinnerungsvermögen des Metalls" liegt offensichtlich bei einer bestimmten Temperatur.
Wenn wir nun die diffusionslose Strukturänderung des Nitinols zugrunde legen, dann würde bei unserem Modell (Abb. 5.67) das Männchen (b) der Hochtemperaturform, dem Ni-Ti-Austenit, entsprechen. Bei Wärmeentzug würde es bei 50°C, der Umwandlungstemperatur, die makroskopische Form aufgrund des Wandels zum Ni-Ti-Martensit annehmen. Es würde niedriger, breiter und schief werden. Bei Wärmezufuhr würde wieder die makroskopische Form wieder die des Männchens (b) entstehen. Über der Temperatur von 50°C wäre demnach das Männchen (b) stabil, unter 50°C das Männchen (c).
Gesetzt den Fall, es gäbe ein Metall, das zuerst vom kubisch flächenzentrierten Gitter zum kubisch raumzentrierten und dann zum schiefen Ni-Ti-Martensit-Gitter wechseln würde: wir könnten dann je nach Temperatur dem Männchen drei verschiedene Formen geben !
Das Prinzip dieser genannten reproduzierbaren Formänderungen ergibt sich aus den unter den Männchen gezeigten Gitterflächen. Die Modellatome 1 bis 4 sind immer an das zentrale Modellatom A geknüpft, bzw. in unmittelbarer Nähe plaziert. Je nach Temperatur werden Bindekräfte wirksam, die eine der drei Formationen festhalten. Wenn sich alle Atome 1 bis 4 um das Atom A quadratisch anordnen, dann erhalten wir Männchen (a). Ordnen sie sich schief an, dann entsteht Männchen (c). Voraussetzung solcher reproduzierbarer Formänderungen ist demnach, daß sich keine Atome wahllos und weiter als ein Atom vom zentralen Atom A wegbewegen, daß also keine Diffusion stattfindet..
In diesem Zusammenhang müssen wir uns aber bewußt machen, daß hinter den Verschiebungen der Teilchen eine ungeheure Kraft steckt. Wenn wir die Änderungen der Positionen der Atome von (a) nach (b) oder (c) aufhalten wollten, dann das nur mit einer für uns ungewöhnlich großen Kraft. Die Teilchen verhalten sich dann so, als würden wir gegen eine starke, gespannte Feder drücken. Insofern erzeugt solch ein Wandel der Kristallstruktur bei einem Einkristall entweder eine neue makroskopische Form ohne mechanische Spannung. Oder wir halten die alte makroskopische Form mit einer großen Gegenkraft fest, sodaß die alte Form unter einer großen mechanischen Spannung steht. In den weiteren Abschnitten werden wir sehen, wie die kleinen Einkristalle mit diesem Problem umgehen.
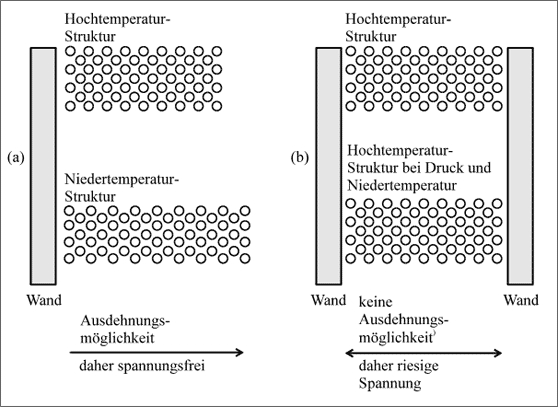
Abbildung 5.68: Modelle zum Zusammenhang von Kristallformen, Kristallstruktur und Materialspannungen
Strukturwandel in polykristallinem Material. Betrachten wir zunächst wieder einen Einkristall in der Hochtemperaturform (Austenit), der einseitig an eine Wand anstößt, dessen Ausdehnungsmöglichkeit aber nicht behindert ist (vgl. (a) in Abb. 5.68): beim Strukturwandel in die Niedertemperaturform (Martensit) wird er sich spannungsfrei ausdehnen. Wenn wir aber den Kristall in der Hochtemperaturform spannungsfrei zwischen zwei festen, durch hohe Kräfte nicht verschiebbaren Wänden plazieren (b), dann wird sich bei der entsprechenden Umwandlungstemperatur die neue Struktur nicht einstellen können. Alle Teilchen im Kristall drücken dann mit einer großen Kraft gegen die Wand wie eine sehr starke Feder. Diese Kräfte können Drücke in der Größenordnung von 100 000 bar erzeugen, wenn im Modell (b) vorausgesetzt wird, daß die Kräfte seitwärts durch Verformung nicht ausweichen können.
In der Praxis sind Einkristalle äußerst selten - im Regelfall der Technik ist ein Metall polykristallin. Das bedeutet, daß die kleinen Einkristalle, die Kristallite, von anderen Kristalliten fest umgeben sind, sie sind von allen Seiten fest eingespannt (vgl. (a) in Abb. 5.69). Bei einem Strukturwandel zu kleinerer Koordinationszahl wird zwar die Höhe des Kristalls etwas kleiner und es wird in dieser Richtung etwas Platz geschaffen, aber in der Querrichtung dehnt er sich mit Macht umso stärker aus. In der Summe benötigt er mehr Platz als vorher.
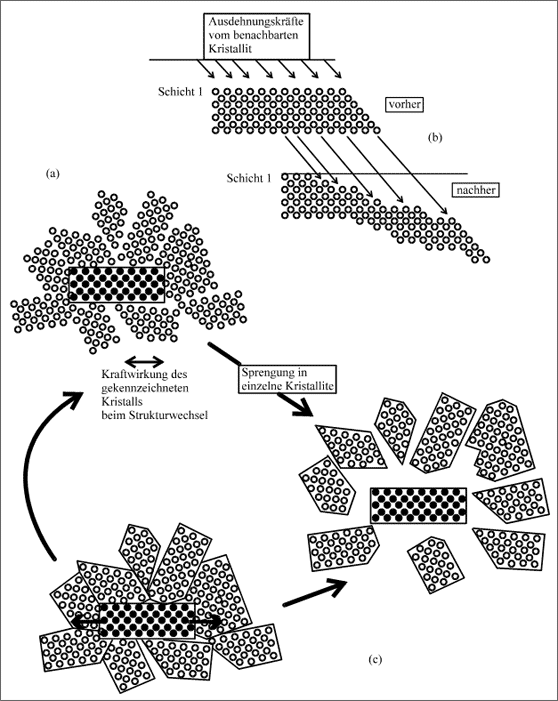
Abbildung 5.69: Modelle für verschiedene Wege, Materialspannungen in Kristalliten abzubauen
Jetzt ist die Frage, wie die Kristallite die Kraftwirkungen durch die Nachbarn auf sich selbst und auf die benachbarten Einkristalle bewältigen - denn schließlich drückt jeder Einkristall auf jeden anderen. Dazu wollen wir uns drei Lösungsmöglichkeiten modellmäßig ansehen: sie laufen alle darauf hinaus, die Spannungen abzubauen. In allen drei Fällen sind die Teilchenverschiebungen mit ihren ungeheuren Kräften nicht aufzuhalten.
Nehmen wir das Eisen als Modellfall, bei dem die Atome sowohl im "Austenit" ( γ-Eisen) als auch im "Martensit" (α-Eisen) reihenweise und flächenweise gut verschiebbar sind (vgl. (b) in Abb. 5.69). Dann ist es naheliegend, daß bei einem Strukturwandel die Kristalle mit ihren Kräften sich gegenseitig Platz schaffen, indem sie die Flächen verschieben, und somit die Kraftwirkungen der Teilchen abbauen. Entscheidend ist dabei aber, daß ganze Schichtpakete verschiedener Dicke über verschieden lange Strecken verschoben werden. Die Chance, alle diese Verschiebungen wieder rückgängig zu machen, ist praktisch Null. Daher wird sich die Form der Kristallite bei jedem Strukturwandel infolge der paketartigen Flächenverschiebungen ständig ändern, eine reproduzierbare Formänderung wie bei einem spannungsfreien Einkristall (vgl. Abb. 5.67) ist nicht möglich. Die makroskopische Form etwa eines Stabes bleibt daher bei einem polykristallinen Material erhalten, obwohl sich Größe, Lage und Form der einzelnen Kristallite geändert haben kann. Die Kristallite arrangieren sich also nach jedem Strukturwandel neu, um die Spannungen im Gefüge der Kristallite möglichst gering zu halten.
Ein weiterer Modellfall der Problemlösung "Spannungsabbau im polykristallinen System" ist das Zinn. Der Übergang vom β-Zinn zum α-Zinn (vgl. Abb. 5.66) entspricht in den Grundzügen dem Wandel des γ-Eisens ins α-Eisen. Allerdings ist der gerichtete Bindungsanteil von Sn-Atomen im α-Zinn so hoch, daß sich die einzelnen Sn-Atome nicht mehr ohne weiteres kollektiv verschieben lassen. Sie trotzen sozusagen den durch Strukturwandel ausgelösten Verschiebungskräften. Damit trifft die Kraftwirkung aber die schwächsten Bindungen im polykristallinen Kristallverband. Das sind die Bindungen an den Randzonen der Kristallite, an denen die Teilchen notdürftig an fehlerhaften Plätzen mit ihren Bindekräften zusammenhalten, was zu halten ist. Die geballte Kraftwirkung bei einer Strukturänderung des Kristallits halten diese Randzonenbindungen aber nicht aus und werden getrennt. Damit wird das polykristalline Zinn in seine einzelnen Kristallite auseinandergesprengt (vgl. (c) in Abb. 5.69): Beim Strukturwechsel vom β-Zinn zum α-Zinn, der bei 13°C stattfindet, zerbröselt das Zinn in selbstzerstörerischer Art zu feinem Zinnstaub: ein schöner Zinnteller - in den Kühlschrank gestellt - ist dahin. Diese Zerstörung des Zinns wurde in früheren Zeiten sehr gefürchtet und deshalb als Zinnpest bezeichnet.
Die eleganteste Methode zum Abbau der beim Strukturwechsel auftretenden Spannungen beobachten wir beim Nitinol. Zunächst betrachten wir gedanklich wieder einen Einkristall, (vgl. (a) in Abb. 5.70): Solange er in der Form des Austenits vorliegt ist er rechteckig, beim spannungsfreien Strukturwandel zum Martensit erhält er die Form eines Parallelogramms. Das ist bisher nichts Neues.
Plazieren wir nun den gedachten Einkristall des NiTi-Austenits mit der Kantenlänge c zwischen zwei Wände, die den Abstand a besitzen (vgl. (b) in Abb. 5.68), dann können sich die ersten drei Titanschichten einschließlich der dazwischen liegenden Ni-Atome nach rechts verlagern, der halbe Kristall hat seine Struktur gewandelt, wobei die oberste Schicht 1 nun an der unverrückbaren Wand anstößt. Sobald nun die Schicht 4 weiter nach rechts drückt (b), schiebt die Wand die Schicht 1 in die entgegengesetzte Richtung nach links zurück, aber ebenfalls in Schieflage, wie es sich für den Martensit gehört. Die Verschiebung der Schicht 5 nach rechts (c) verursacht die Verschiebung von Schicht 2 nach links und die weitere Verschiebung von Schicht 6 nach rechts wird durch die Verschiebung von Schicht 3 nach links in Schieflage kompensiert. Damit hat sich die Struktur bei gleichzeitiger "Faltung" gewandelt.
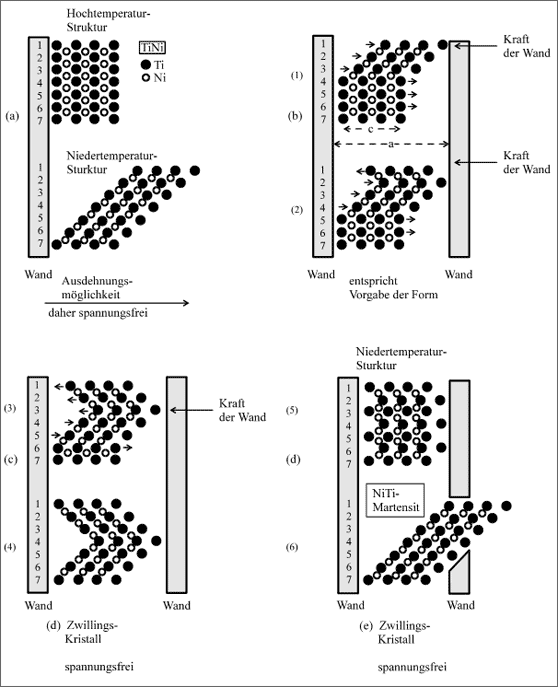
Abbildung 5.70: Modellvorstellungen für den Abbau von Materialspannungen in Kristalliten des Nitinol
Einen solchen "gefalteten" Kristall nennt man auch einen Zwillingskristall oder kurz Zwilling. Er ist spannungsfrei, weil die Teilchen ihre Verschiebekräfte zu zwei Seiten kompensieren konnten.
In unserem Gedankenexperiment verringern wir vor der Strukturwandlung den Abstand a der beiden Wände so, daß bereits die Schicht 1 nach der Verschiebung an der rechten Wand anstößt (vgl. (d) in Abb. 5.70). Jetzt wird bereits die Schicht 2 bei ihrer Verschiebung nach rechts die Schicht 1 nach links verschieben, die dann wieder an der linken Wand anstößt. Die Verschiebung der Austenitschicht 3 nach rechts schiebt die Schicht 2 nach links, die Schicht 1 wieder nach rechts. Auf diese Weise wird der Kristall anhand seiner Umwandlung wie eine Zieharmonika "gefaltet". Dieser Kristall in der Martensitstruktur ist spannungsfrei und in der makroskopischen Form nicht sehr von seiner ursprünglichen Austenitform verschieden. Zum Vergleich zeigt (d) noch einmal den gestreckten Martensit-Kristall im Modell.
Die "Faltung" eines Kristalls ist immer dann möglich, wenn wir von seiner Kristallstruktur ein Spiegelbild anfertigen können, das mit seinem Original nicht zur Deckung zu bringen ist. In der Fläche zeigt dies der Vergleich zwischen einem flächenzentrierten Quadrat und dem flächenzentrierten Parallelogramm, einer schematisierten Gitterfläche des NiTi-Martensits (vgl. Abb. 5.71). Die Quadrate (a) erzeugen Spiegelbilder, die dem Original völlig gleich sind, gleichgültig, ob wir über die Kante oder Ecke spiegeln. Wie auch immer wir nach einem der vier Quadratmuster bauen, wir erhalten immer gleiche Flächen, die zur Deckung gebracht werden können.
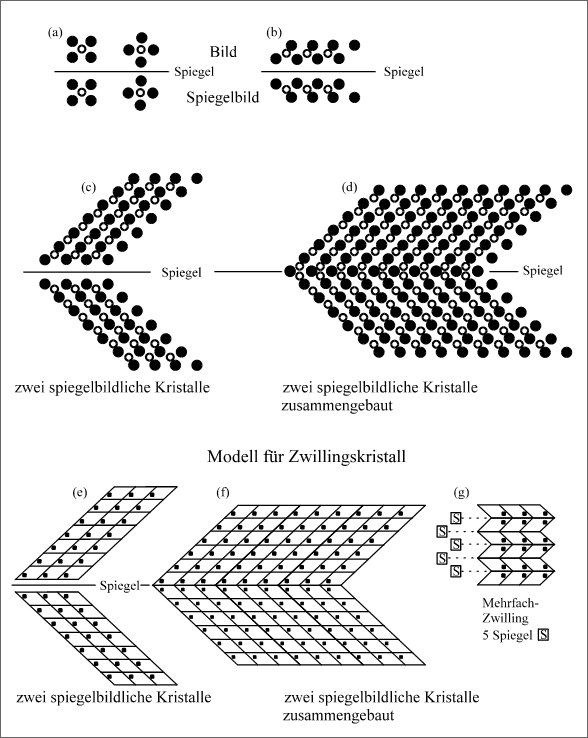
Abbildung 5.71: Modelle zur Beschreibung von Zwillingskristallen
Die Spiegelung der schiefen Flächen (b) ergibt ein Spiegelbild, das wir durch Drehen nur in der Papierebene nicht zur Deckung bringen können. Nun können wir nach dem gleichen Baumuster zwei verschiedene, spiegelbildliche Kristallflächen aufbauen (c). Werden zwei spiegelbildliche Kristalle von einem gemeinsamen Muster aus aufgebaut wie in (d), dann nennt man den entsprechenden Kristall einen Zwilling. Die Kugelfläche, die zu beiden Spiegelbildern gehört, wirkt als Spiegel und wird Zwillingsebene genannt.
Die gleichen Verhältnisse sind nochmal symbolisch in geometrischen Figuren (e) und (f) dargestellt, wie sie häufig verwendet werden. Die Figur (g) symbolisiert einen Mehrfachzwilling, wie er modellmäßig bereits in (d) der Abbildung 5.70 dargestellt wurde. Bei all diesen Modellen ist in Bezug auf die Originalkristalle festzuhalten, daß die spiegelbildlichen Kristallgitter keine veränderten Stoffeigenschaften hervorrufen, also die Substanz jeweils erhalten bleibt, da sowohl die Strukturen der Teilchenverbände als auch die die Teilchen zusammenhaltenden Bindekräfte erhalten bleiben.
Formgedächtnis. Im vorhergehenden Abschnitt haben wir Kraftwirkungen auf einen Kristallverband als Folge der Umwandlung von Kristallstrukturen betrachtet. Wie wir gesehen haben, werden Eisenkristalle in sich verschoben, α-Zinnkristalle auseinandergesprengt und NiTi-Kristalle zu Zwillingskristallen gefaltet.
Nun stellen wir die umgekehrte Frage: Was geschieht, wenn wir auf einen polykristallines Kristallgefüge von außen gleichmäßig Kräfte einwirken lassen? Die Frage ist einfach zu beantworten: Es geschieht im wesentlichen das gleiche wie bei der Kraftbeanspruchung von innen. Eine typische Krafteinwirkung von außen auf die Kristallite ist das Verbiegen eines Stabes (vgl. Abb. 5.72). An der Außenseite der Biegung sind Kristallite gezogen, auf der Innenseite sind sie zusammengedrückt worden.
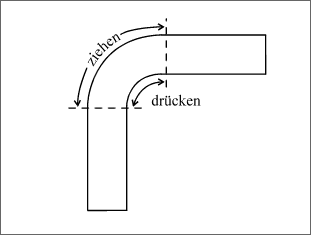
Abbildung 5.72: Modell eines gebogenen Metallstabes
Eisenkristallite setzen die Kraftwirkungen in diesem Fall in die bekannten Verschiebungen der Teilchenschichten um. Ein α-Zinnstab wird an der Außenseite reißen und auf der Innenseite bröseln, weil die Kristallite aus ihrem Gefüge gerissen werden. Bereits beim normalen β-Zinn werden durch das Biegen Kristallite so aneinander vorbeigezerrt, daß der Biegeprozeß von einem eigenartigen, knirschenden Geräusch begleitet wird. Unsere Vorväter nannten dieses Geräusch "Zinngeschrei".
Ein Stab aus NiTi bei niedriger Temperatur (unter 50°C) in der "schiefen" Martensitstruktur verhält sich gegen die anderen beiden Metalle Eisen und Zinn richtig pfiffig, wenn er gebogen wird. Auf der Innenseite, der Druckseite, werden Kristalle gefaltet, die es bisher nicht waren. Auf der Außenseite werden Kristalle, die gefaltet waren, auseinander gezogen. Der Fachmann spricht in diesem Zusammenhang von Zwillingsbildung und Zwillingsauflösung. Ein dazu passendes Modell wäre der Ziehharmonikaspieler, der während des Spielens seine Harmonika immer wieder rund auseinander zieht und rund zusammendrückt.
Das Entscheidende bei dieser Verformung ist, daß sich im Gegensatz zu den beiden anderen Metallen die Zuordnung der einzelnen Atome zueinander nicht ändert. Denn ein Zwilling läßt sich wie ein Scherengitter auffalten und wieder erneut falten. Das gilt aber nur für die Niedertemperaturform NiTi-Martensit.
Die Hochtemperaturform NiTi-Austenit mit ihrem kubisch innenzentrierten Gitter verhält sich zunächst bei Druckbeanspruchung durch Verformung analog dem Eisen. Teilchenflächen und Teilchenreihen werden so verschoben, daß die Kristalle der neuen makroskopischen Form wieder ein geordnetes, innenzentriertes Gitter aufweisen. Die Spannungen sind dann weitgehend abgebaut.
In der Abbildung 5.73 sind beide NiTi-Strukturen noch einmal in Form der Flächen gegenübergestellt worden. Man erkennt, in welcher Weise der Austenit (1a) durch Scherung in den Martensit (2a) übergehen kann. Wenn er aber zwischen anderen Kristallen eingeklemmt ist, wird er sich nach (3a) falten lassen. Die makroskopische Form (1a) ist nicht sehr von der makroskopischen Form (3a) verschieden, sodaß bei der Strukturänderung nur mäßige Spannungen überbleiben.
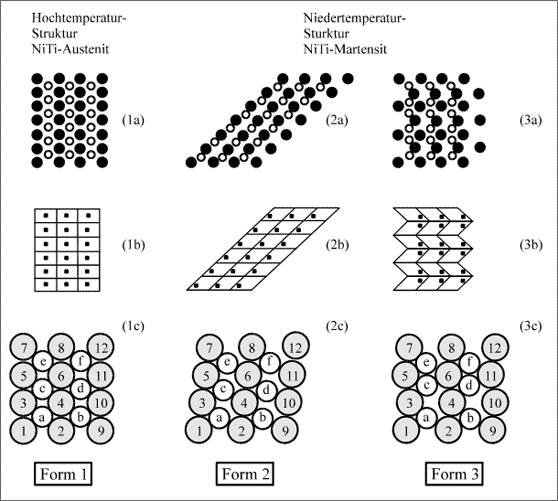
Abbildung 5.73: Modellvorstellungen zum Strukturwechsel des NiTi-Austenit und NiTi-Martensit
Die Modelle und Symbole der Reihe (b) in Abbildung 5.73 zeigen den gleichen Sachverhalt wie die der Reihe (a). Die Streckung des Kristalls (2b) und die Faltung (3b) sind allerdings in dieser Darstellung besser erkennbar, außerdem sind die Modelle (1b) und (2b) leichter zuzuordnen. Die Reihe (c) zeigt die Positionen der Atome anhand der realen Verhältnisse der Durchmesser und dem richtigen Scherwinkel von 8°. Der Scherwinkel der Modelle (2a) und (2b) ist dagegen willkürlich.
Alle drei Modelle (1c), (2c) und (3c) lassen die Umgebung der kleineren Ni-Atome gut erkennen. Die Ni-Atome sind mit Buchstaben, die Ti-Atome mit Zahlen versehen. Man kann sich selbst davon überzeugen, daß die Zuordnung derselben Atome in den drei Strukturen jeweils gegeben ist. Das Ni-Atom a ist beispielsweise in allen drei Fällen von den Ti-Atomen 1,2,3 und 4 umgeben. Eine mit der Temperatur veränderbare Kräftewirkung kann daher leicht durch eine kleine Teilchenverschiebung aus der Struktur (1c) die Strukturen (2c) und (3c) werden lassen und umgekehrt. Wenn aus der Teilchenanordnung des Martensits (2c) oder (3c) die Anordnung des Austenits (1c) wird, dann ist auch aus der makroskopischen Form 2 oder Form 3 die makroskopische Austenitform 1 geworden.
Das ist nun der Hintergrund des Metalls Nitinol mit "Erinnerungsvermögen" an eine frühere Form. Die Ausgangsform 1 wird bei höherer Temperatur mit der Struktur des Austenits hergestellt (vgl. (1) in Abb. 5.73), beispielsweise ein polykristalliner, gerader Stab. Bei Wärmeentzug unter eine Temperatur von 50°C klappt das Gitter aller eingespannter Kristallite im Stab zum "schiefen" Gitter des Martensits um. Die Spannungen werden durch Faltung oder Zwillingsbildung (3) der Kristallite abgebaut, die makroskopische Form des Stabes bleibt erhalten. Wird der Stab gebogen, dann bilden sich neue Zwillinge (3) oder es werden Zwillinge entfaltet (2). Diese Martensitkristallite im Stab sind stabil und halten die gebogene Form des Stabes aufrecht. Wird der gebogene Stab dann auf 50°C erwärmt, so ändern die Kristallite unter Wärmeaufnahme ihre Struktur wieder in die des Austenits. Da sich die Zuordnung der Atome zueinander während des ganzen Prozesses nicht ge-ändert hat, muß der Stab seine gerade Form wieder zurückerhalten: Atom 3 auf Platz 3, Atom 5 auf Platz 5, usw.
In Abbildung 5.74 werden die Vorgänge schematisch zusammengefaßt. Die Form A wird bei höherer Temperatur mit Austenitgitter hergestellt. Bei tieferer Temperatur wandelt sich der Austenit in Martensit um und wird verzwillingt. Die makroskopische Form A' gleicht mit guter Näherung der ursprünglichen Form A. Bei Verformung zur Form B wird die martensitische Struktur nicht geändert, lediglich die Lage der Zwillinge. Bei erneutem Erwärmen über 50° wird die Struktur des Austenits wieder zurückgebildet und somit die ursprüngliche Form A.
Um die Sachlage etwas bildhafter zu gestalten, ist sie in der Abbildung 5.74 an einem großen Buchstaben R schematisch dargestellt. Zunächst erkennt man das R im quadratischen Muster des Austenits bei einer Temperatur über 50°. Beim Abkühlen und Wärmeentzug klappt das Gitter in den schiefen Martensit um, die Form des R bleibt erhalten. Man kann das R nun verbiegen, dabei falten sich viele Zwillinge auf, andere bilden sich neu. Die Struktur und Zuordnung der kleinen Parallelogramme ist noch zu erkennen. Werden nun aus diesen Parallelogrammen bei einer Temperatur über 50° wieder Quadrate, dann erhalten wir das R in der Anfangsform zurück.
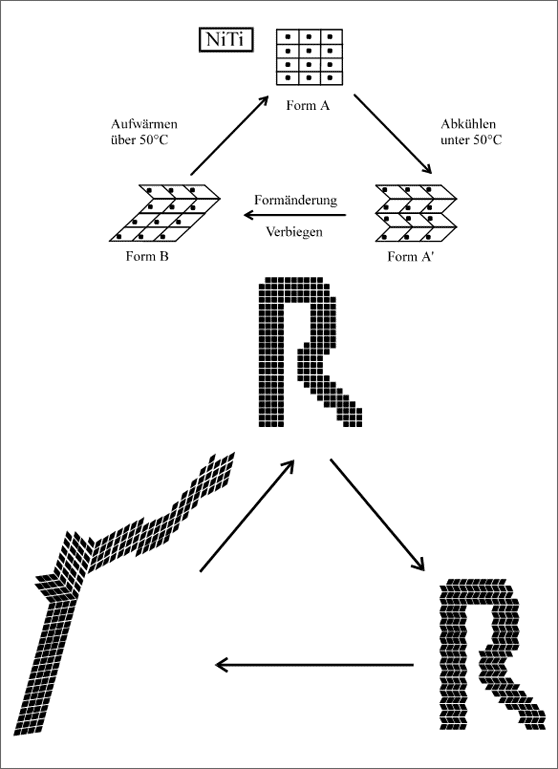
Abbildung 5.74: Schematische Modelle für das Formgedächtnis der Memorymetalle, Beispiel Nitinol
Diese Memory-Legierungen werden in der Technik vielseitig angewandt. Gebogene Stäbe, die als Haken dienen, klinken Sateliten aus Trägerraketen aus, wenn Wärme zugeführt wird. Fertige, feinmaschige Drahtnetzantennen aus Nitinol faltet man zum Transport auf kleinem Raum zusammen und entfaltet sie vor Ort wie eine Blume durch leichtes Erwärmen. Aus der alltäglichen Konstruktionstechnik für Steck- und Klemmverbindungen, für Federn und Schalter sind die Memory-Metalle nicht mehr wegzudenken. Um den Energieumsatz des Strukturwandels energetisch zu nutzen, sind sogar kleine "Motoren" konstruiert worden.
![]()


