5.2.3.4 Intermetallische Verbindungen
Besitzt eine Intermetallische Phase einen sehr engen Homogenitätsbereich, dann wird diese Kristallsorte als Intermetallische Verbindung bezeichnet. Ein enger Homogenitätsbereich heißt letztlich, daß die Variation der Zusammensetzung der Kristallsorte nicht mehr gegeben ist: Die Kristallsorte erfordert deshalb immer ein strenges, festgelegtes Teilchenzahlenverhältnis. Beide Teilchenarten können nicht mehr statistisch zusammengebaut, sie müssen geordnet sein. Eine solche Intermetallische Verbindung besitzt deshalb eine konstante Schmelztemperatur.
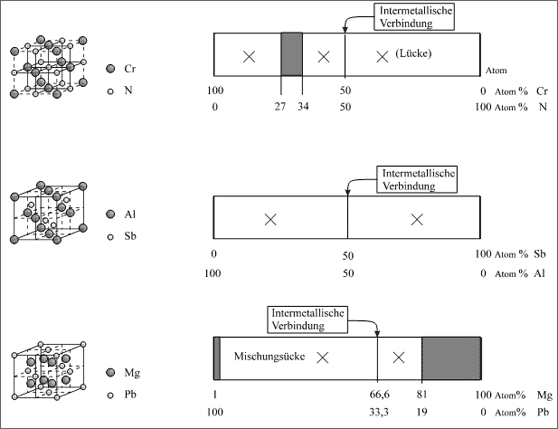
Abbildung 5.49: Intermetallische Verbindungen, Beispiele Cr/N-, Al/Sb- und Mg/Pb-System
![]()
Beispiel Cr/N. Die Verbindung von Chrom und Stickstoff liefert drei verschiedene Phasen. Chrom für sich allein kristallisiert kubisch raumzentriert. Ähnlich wie Eisen bilden die Cr-Atome mit ganz wenigen N-Atomen zusammen im Bereich bis 0,4 Atom% N Mischkristalle. Im Bereich zwischen 27 und 34 Atom% N bilden die Cr-Atome eine hexagonal dichteste Kugelpackung, wobei die N-Atome in die Oktaederlücken eingelagert werden. Bei 33,3 Atom% N ist jede zweite Lücke gefüllt, das Zahlenverhältnis von Cr- zu N-Atomen muß dann 2:1 sein.
Bei höherem N-Angebot bilden die Cr-Atome eine kubisch dichteste Packung mit völliger Besetzung der Oktaederlücken. Wir erhalten die Struktur, die uns bei der Einlagerung von C-Atomen schon begegnet ist (vgl. Abb. 5.43 und Abb. 5.49). Das dazu erforderliche Teilchenverhältnis 1:1 ist praktisch nicht variierbar. Daher wird diese Phase als Intermetallische Verbindung bezeichnet. Sie erscheint im Konzentrationsband als Strich bei 50 Atom% (vgl. Abb. 5. 49), ihr kann das Symbol Cr1N1 oder CrN zugeordnet werden.
Beispiel Al/Sb. Aluminium und Antimon bilden keine Mischkristalle, obwohl die Atomradien fast gleich sind. Die niedrigen Schmelztemperaturen von ca. 650 °C deuten wir als schwache Kräfte zwischen den gleichen Teilchenarten. Man stellt allerdings im Experiment fest, daß in einem Aluminium-Antimon-Kristall regelmäßig vier Al-Atome um ein Sb-Atom und vier Sb-Atome um ein Al-Atom gebunden sind, also ein Teilchenzahlenverhältnis von 1:1 vorliegt. Die Kräfte zwischen Al-Atomen und Sb-Atomen scheinen also stark zu sein.
Dieser Kristall existiert auch tatsächlich nur bei dieser Konzentration. Die Al-Atome bilden die Anordnung der kubisch dichtesten Packung und die Sb-Atome besetzen die Plätze jeder zweiten Tetraederlücke. Auch hieraus ersehen wir das Zahlenverhältnis 1:1. Wie das Konzentrationsband zeigt (vgl. Abb. 5.49), besteht das ganze System Al/Sb nur aus drei Phasen: Reines Aluminium, reines Antimon und Intermetallische Verbindung bei 50 Atom%. Sie schmilzt bei der hohen Temperatur von 1070°C und zeigt somit die gegenseitige starke Bindung der Al- und Sb-Atome an.
Beispiel Mg/Pb. Ein Vergleich der Schmelztemperaturen, der Oberflächenspannungen und anderer Daten läßt folgendes Kräfteschema vermuten: Mg-Mg - starke Bindungskräfte, Pb-Pb - schwache Kräfte, Pb-Mg - starke Kräfte.
Wie das Experiment zeigt, scheinen die Kräfte in einer Verbindung zwischen Pb- und Mg-Atomen am besten ausgeglichen zu sein, wenn 8 Mg-Atome um 1 Pb-Atom und 4 Pb-Atome um 1 Mg-Atom gruppiert sind. Die Kraftwirkungen eines Pb-Atoms müssen demnach doppelt so groß sein wie die eines Mg-Atoms, in dem Kristall sind doppelt so viele Mg-Atome wie Pb-Atome gebunden. Neben anderen Mischkristallen gibt es also eine Intermetallische Verbindung mit 66,6 Atom% Mg (vgl. Abb. 5.49), ihr Symbol lautet PbMg2.
Die Struktur dieser Intermetallischen Verbindung, die Mg- und Pb-Atome im Zah-lenverhältnis 2:1 enthält, läßt sich wiederum von der kubisch flächenzentrierten Struktur ableiten: Die Pb-Atome ordnen sich in Form der kubisch dichtesten Packung an, alle Tetraederlücken sind durch Mg-Atome besetzt (vgl. Abb. 5.49). Wohlgemerkt, die Pb-Atome bilden keine dichteste Packung, sie berühren sich selber nicht: Die Lücken wären für die Mg-Atome viel zu klein.
Beispiel Fe/C. Im Kombinationssystem Fe/C tritt neben den Mischkristallen eine Intermetallische Verbindung auf, die bei vielen Stahlsorten als kristalliner Bestandteil eine große Rolle spielt: Sie wird Zementit genannt. Die Schmelztemperatur liegt bei 1837°C, wobei der Kristall in der Regel vor seinem Schmelzen in Eisen und Kohlenstoff zerfällt. Die Kristalle enthalten 25 Atom% C, das Zahlenverhältnis der Atome Fe:C beträgt also 3:1, das Symbol lautet Fe3C.
Neben dem Zementit ist Austenit ein bei höheren Temperaturen existierender Mischkristall des Fe/C-Systems, der bis zu 8 Atom% C enthalten kann (vgl. Abb. 5.50). Die Intermetallische Verbindung Zementit wird im Konzentrationsband bei genau 25 Atom% C registriert und hebt sich deutlich durch eine Mischungslücke vom Austenit ab (vgl. Abb. 5.50).
Zementit besitzt - verglichen mit reinem Eisen - eine sehr große Härte. Das hängt mit der Gitterstruktur zusammen, die keine Gleitebenen aufweist und ein einfaches Verschieben von Atomreihen nicht zuläßt. Die Fe-Atome im Zementit bilden keine dichteste Kugelpackung mehr, wie im γ-Eisen oder Austenit. Die Struktur ist aber ableitbar von der hexagonal dichtesten Kugelpackung, in der Eisen bei Zimmertem-peratur ab einem Druck von 130 000 bar stabil ist. Substituiert man in dieses ε-Eisen 10% der Fe-Atome durch Mn-Atome, dann bleibt die hexagonal dichteste Kugelpackung bis zu Zimmertemperatur auch bei Normaldruck erhalten. Der Einbau von C-Atomen wirkt offensichtlich in der gleichen Richtung.
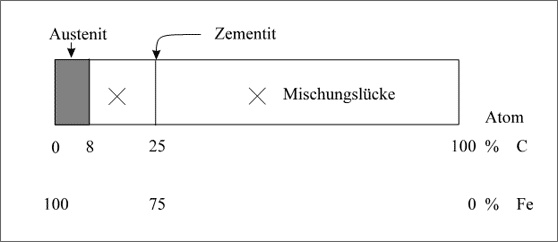
Abbildung 5.50: Intermetallische Verbindung Zementit im Fe/C-System bei etwa 1000 oC
Die ebenen Schichten der Fe-Atome einer normalen dichtesten Kugelpackung finden wir im Zementit nicht mehr. Die Schichten der Zementitstruktur können wir jedoch als gefaltete dichteste Schichten auffassen und von den ebenen Schichten mit Sechseckmuster ableiten. Dazu betrachten wir eine dichtest gepackte Schicht (vgl. (a) in Abb. 5.51)
Wenn wir uns vorstellen, daß die Schicht auf der linken Seite blockiert ist und in Pfeilrichtung von rechts eine Kraft einwirkt, dann können beispielsweise die mit einem schwarzen Kreis gekennzeichneten Kugeln nach unten und die mit einem schwarzen Quadrat gekennzeichneten Kugeln nach oben ausweichen. Damit sackt gleichzeitig die ganze Kugelreihe der schwarzen Punkte etwas nach unten und die Kugelreihe der schwarzen Quadrate hebt sich etwas nach oben. Auf diese Weise wird die Fläche gleichmäßig gefaltet und verkürzt
Die ganze Fläche gleicht nach dem Faltvorgang der Oberfläche eines Kartoffelfeldes mit den Furchen. Der senkrechte Schnitt zur Furchenrichtung ist mit der Vorderansicht unserer gefalteten Schicht zu vergleichen, wobei die Knickgeraden zur Orientierung mit Tal und Kamm bezeichnet sind (vgl. (b) - (e) in Abb. 5.51). Insbesondere in (c) ist zu erkennen, daß erst jeweils zwei Reihen zusammen betrachtet die "Furchen eines Kartoffelfeldes" widerspiegeln, daß die Kugeln der Reihe 1 alle etwas niedriger liegen als die der Reihe 2. Figur (d) verdeutlicht die unterschiedlichen Höhen der Kugelmittelpunkte in der gefalteten Lage der Kugeln: Die Höhe des Tals ist mit 1, die des Kammes mit 4 gekennzeichnet. Figur (e) zeigt schließlich den im Zementit tatsächlich gemessenen Winkel von 112°.
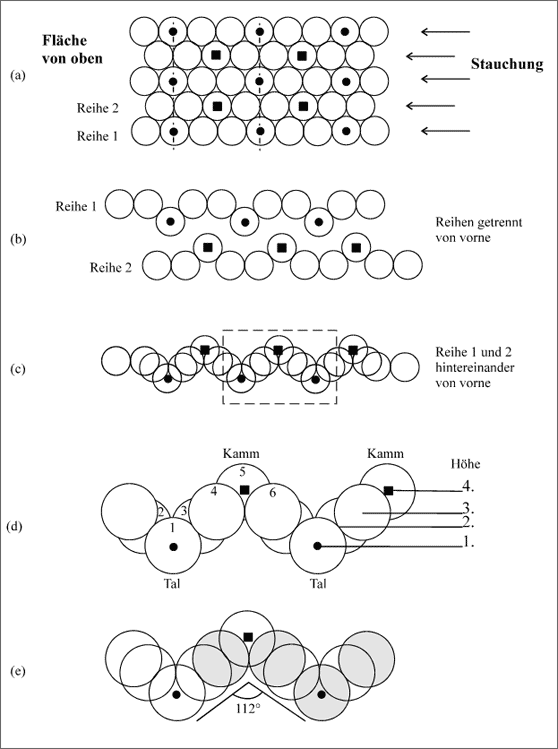
Abbildung 5.51: Modellvorstellungen für gefaltete Schichten von Fe-Atomen im Zementit
Einen anderen Eindruck des Faltgeschehens erhält man, wenn Modelle zu Bändern dichtest gepackter Kugeln tatsächlich gebaut werden, wie sie Figur (a) in Abbildung 5.52 zeigt. Wir kombinieren sie zu einer ebenen, dichtesten Fläche (b), wobei Kugeln der Nahtstelle, die zum Band der Seite 1 gehören, im Bild mit einem Sternchen und schwarzer Umrandung gekennzeichnet sind. Durch die Mittelpunkte dieser Kugeln soll die Knickgerade laufen, sie liegt in Bezug auf die beiden kombinierten Bänder unsymmetrisch - um eine Lücke verschoben - zum Band der Seite 1. Wir belegen diese Schicht mit zwei weiteren gleichen Bändern (in (b) schraffiert gezeichnet), so daß zwar Band auf Band in Art einer dichtesten Kugelpackung zu liegen kommt, jedoch zwischen den Bändern eine exakte Kugelreihe frei bleibt.
Die zweite Schicht verursacht bekanntermaßen Tetraeder- und Oktaederlücken. Während die Tetraederlücken geschlossen sind, erweisen sich alle Oktaederlücken noch unvollständig. Beispielsweise bilden die Kugeln der unteren Schicht 1,2,3 mit den Kugeln 4 und 5 der oberen Schicht einen offenen Oktaeder, der durch eine Kugel in der Position 6 geschlossen werden könnte (vgl. (b) der Abb. 5.52). Die Kugeln 1,2,5,4 bilden ein Quadrat, das zum genannten Oktaeder gehört. Solche Formationen finden wir auf beiden inneren Seiten der Streifen entlang der Knickgeraden. Auf der Seite 2 bilden etwa die Kugeln der unteren Schicht 9,10,11 zusammen mit denjenigen der oberen Schicht 12,13 eine weitere, offene Oktaederlücke.
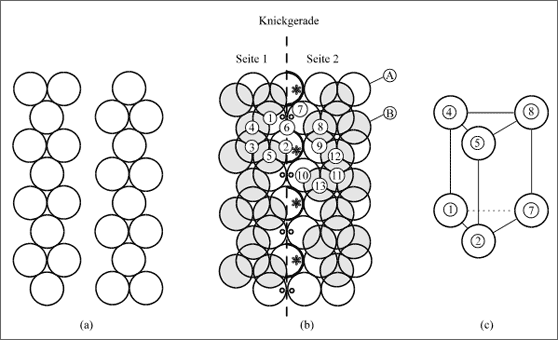
Abbildung 5.52: Modellvorstellungen für das Entstehen von trigonalen Prismen als Lücken für C-Atome ![]()
Wenn man nun die beiden Seiten mit der Knickgeraden als Drehachse nach oben kippt, dann rollen die Kugeln 1 und 7 und alle entsprechenden mit einem dunklen kleinen Kreis gekennzeichneten Kugeln der unteren Schicht aneinander ab, bis sich die Kugeln der beiden aufgesetzten Bänder berühren. Die unsymmetrische Lage der Knickgeraden bewirkt, daß die beiden Kugeln 7 und 8 in die Lücken zwischen den Kugeln 1, 2 und 4, 5 des Quadrats 1, 2, 5, 4 einrasten und damit ein trigonales Prisma 4,5,8; 1,2,7 bilden (vgl. (c) in Abb. 5.52). Dieses enthält eine bedeutend größere Lücke als ein Oktaeder und kann ein C-Atom ohne Schwierigkeiten aufnehmen.
In unserem Modell (vgl. (b) in Abb. 5.52) werden die mit Sternchen gekennzeichneten Atome in der Knickgeraden einseitig nach unten gedreht und bilden die "Talkugeln". Dabei vergrößern sich infolge des gegenseitigen Wegdrehens der Talkugeln von den Kugeln der Seite 2 die Abstände erheblich - auch dies ist ein Anzeichen dafür, daß die Faltung der Schichten die dichteste Packung auflockert. Da die mit Sternchen gekennzeichneten Talkugeln nach unten abgedreht worden sind, neigen sich die Grundflächen der trigonalen Prismen in Richtung der Knickgeraden, im speziellen Fall weist die Fläche1,2,7 einen Winkel zur Papierebene auf.
Es ist zu wiederholen, daß die offenen Oktaederlücken auf der Seite 1 des aufgesetzten Bandes nicht durch eine Kugel zum Oktaeder, sondern durch zwei Kugeln zum trigonalen Prisma geschlossen werden (vgl. (c) in Abb. 5.52). Anders verhält es sich auf der Seite 2. Durch die unsymmetrische Lage der Knickgeraden, die das aufge-setzte Band der Seite 2 um eine Lücke weiter nach außen verlagert, rastet eine Kugel der Seite 1 beim Falten in den Mittelpunkt des Quadrats auf der Seite 2 ein, die Kugel 5 etwa rastet in das Quadrat 9,10,12,13 ein und schließt einen Oktaeder. Wenn eine Kugelpackung nach dem angegebenen Schema gefaltet wird, so ist sie anhand einer Kombination von Tetraeder-, Oktaeder- und trigonal prismatischen Lücken beschreibbar - sie ist dann nicht mehr dichtest gepackt.
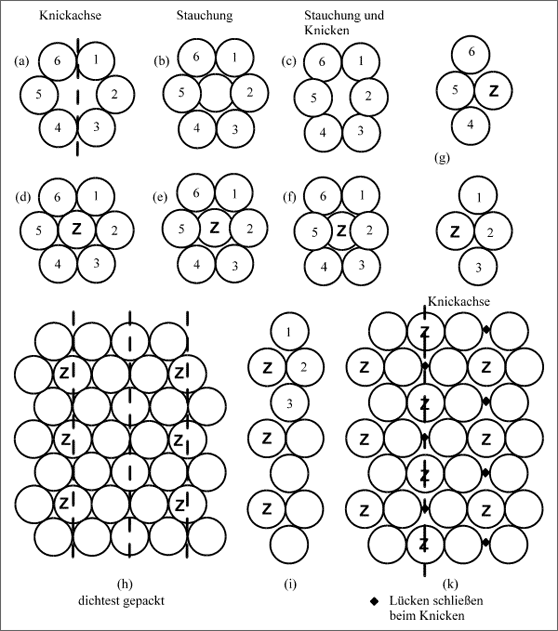
Abbildung 5.53: Stauchung und Faltung einer dichtest gepackten Kugelschicht mit Hilfe von Zentrumskugeln Z
In zwei wesentlichen Punkten weicht allerdings unser Modell von den experimentellen Meßdaten ab. Der theoretische Faltwinkel des Modells ist 117°, am echten Zementit werden allerdings 112° gemessen. Diese Abweichung ist darin begründet, daß die Kugelbänder, die wir für unser Modell verwendet haben, ebenfalls in der Ebene der Bänder nicht dichtest gepackt sind: sie ändern bestimmte Atomabstände nach einem vorgegebenen Muster, was letztlich den Faltwinkel von 112° bestimmt.
Wir verfeinern unser Modell der Faltung in der Art, wie es in Abbildung 5.53 dar-gestellt ist. Dabei gehen wir vom Sechsring einer dichtest gepackten, ebenen Schicht aus, bei der das Zentrumsatom fehlt (a). Bei der Stauchung senkrecht zur Knickachse wird jetzt zunächst der Sechsring etwas zusammengedrückt (b), er wird dadurch etwas schmaler und gleichzeitig höher. Der ursprüngliche Winkel von 120° zwischen allen Ringatomen wird zwischen den Atomen 1,2,3 und 4,5,6 größer, zwischen den anderen Atomen kleiner. Die zusätzliche Knickung zeigt (c). In (d) wird das Zentrumsatom Z mit berücksichtigt, das bei der Stauchung nach unten ausweicht (e). Dabei wird der Abstand der Atome 6,1 und 3,4 zum Zentralatom Z vergrößert, nur noch die Atome 2 und 5 berühren nach wie vor das Zentralatom. Folgt anschließend die Knickung (f), dann weicht das Zentralatom noch weiter nach unten aus. Während sich der Abstand der bereits weiter entfernten Atome 1,3,4,6 noch zusätzlich vergrößert, bleibt die Berührung der Atome 2 und 5 zum Zentralatom erhalten. Der Winkel zwischen den Atomen 2-Z-5 beträgt nun 112°.
Die Atome 1,2,3,Z liegen wie die Atome 4,5,6,Z jeweils in einer Ebene. Projiziert man diese Ebenen senkrecht auf das Papier, dann entstehen die Figuren (g). Es ist deutlich ersichtlich, daß der Abstand zwischen dem Zentrumsatom Z und den Atomen 1 und 3 bzw. 4 und 6 erheblich vergrößert ist. Wir könnten das Flächenmuster der geknickten Fläche so in eine Ebene zurückverwandeln, daß die Aufweitungen zwischen den Teilchen erhalten bleiben. Damit ist ein Vergleich mit einer dichtest gepackten ebenen Schicht möglich (vgl. (h) in Abb. 5.53). Reihen wir die kleinen, aufgeweiteten Flächen (g) aneinander, so erhalten wir ein aufgeweitetes Band (i), zusammengesetzt zu einer ebenen Fläche (k). Die Aufweitungen der Abstände zwischen den Teilchen links und rechts der Knickachse sind mit einem Sternchen versehen. Sie verschwinden beim Knicken, sodaß sich im gefalteten Zustand alle Teilchen in einer Reihe senkrecht zu den Knickachsen berühren. Der Raumbedarf, der durch diese Erweiterung angedeutet wird, bleibt aber erhalten, sobald man die gefalteten Schichten stapelt.
Die Zentrumskugeln Z entsprechen in einer Knickachse einem Tal und in der nächsten einem Kamm. Werden diese durch Modellkugeln gleicher Größe dargestellt, dann berühren die Kugeln Z diejenigen der benachbarten Reihen nicht, das muß man beim Bau solcher Schichten berücksichtigen. Der Kristallograph bewertet die Aufweitung von etwa 7% des Durchmessers zwischen diesen Atomen lediglich als Abstandsvergrößerung, die nur einen geringen Verlust an Bindungskraft zwischen den Atomen verursacht. Trotz ungleicher Bindungsabstände wird dem Zentrumsteilchen, ob Tal oder Kamm, in der Formation (k) der Abbildung 5.53 die Koordinationszahl sechs zugewiesen.
Eine nach unseren Vorgaben gefaltete Schicht zeigt von oben die Ansicht, wie sie (a) in Abbildung 5.54 wiedergibt. Sie erinnert zwar noch stark an die dichtest gepackte ebene Schicht, sie ist es aber nicht: (b), (c) und (d) zeigen dies sehr deutlich. Die Dreiecksmaschen in den Tal- und Kammlagen sind in (b) gesondert herausgestellt, wie sie sich übereinander schichten, zeigen (c) und (d). In diesen Bildern gibt die Verbindung der Punkte M die Faltgerade an, der Wechsel von Kamm- und Tallagen ist zu erkennen: jeweils Tal- und Kammlagen sind durch genau eine Kugel dargestellt, die Kugelpaare besetzen die Höhen 2 oder 3 (vgl. (a) in Abb. 5.54). Die bei der Stapelung entstehenden trigonalen Prismen sind sowohl in der Tallage (c) als auch in der Kammlage (d) auf den Betrachter zu geneigt: sie nehmen die C-Atome auf.
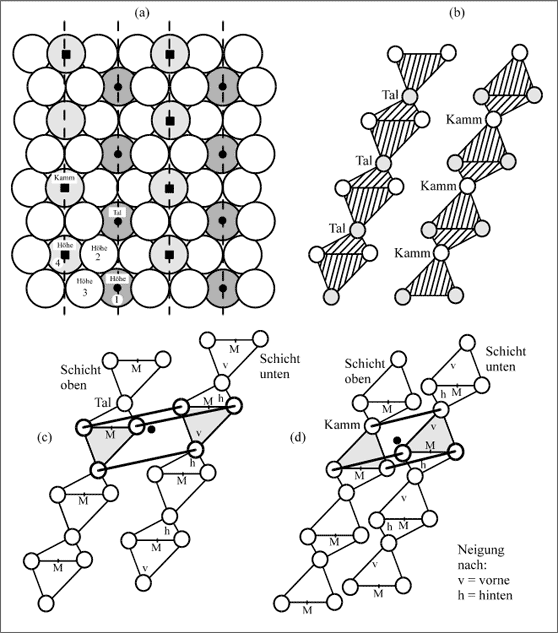
Abbildung 5.54: Modellvorstellungen für gefaltete Schichten von Fe-Atomen im Zementitgitter![]()
Im Zementit sind solche Schichten von Fe-Atomen in der Abfolge ABAB, ähnlich einer hexagonal dichtesten Kugelpackung, gestapelt. Die folgende Schicht wird dabei in Richtung der Knickgeraden um einen Kugelradius verschoben, wie es in Abbildung 5.55 skizziert ist: von der zweiten Schicht ist eine Dreiecksmasche in Tallage und eine in Kammlage schraffiert eingezeichnet worden. In beiden Fällen erkennt man wiederum die Formationen der prismatischen Lücken zur Aufnahme der C-Atome.
Diese Prismen werden aber auf einer gefalteten Schicht immer nur auf den Kämmen oder in den Tälern von den Dreiecksmaschen einer Neigung gebildet. Da in den Tälern und auf den Kämmen die Neigung der Dreiecksmaschen ständig abwechselt, kann nur jede zweite Lücke dieser Dreiecksmaschen mit einem C-Atom besetzt werden. Dies zeigt Abbildung 5.55: Die Positionen der besetzten Lücken sind mit A bezeichnet, die unbesetzten mit B.
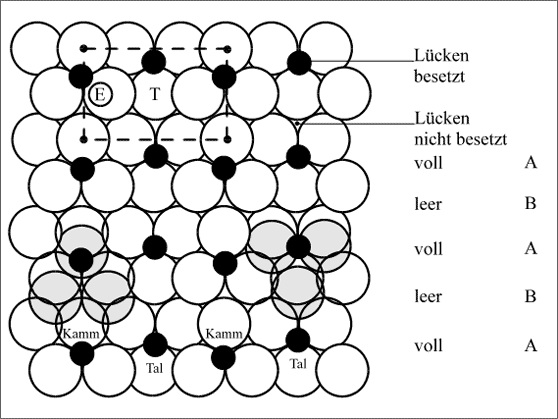
Abbildung 5.55: Abfolge der gefalteten Schichten von Fe-Atomen und Besetzung mit C-Atomen
Bei der Stapelung der Schichten muß die dritte Schicht mit der ersten wieder identisch sein, dementsprechend ist die Verschiebungsrichtung der dritten Schicht ent-gegengesetzt zur zweiten zu wählen. Somit werden die Dreiecksmaschen mit der Gegenneigung zu trigonalen Prismen geformt und mit C-Atomen besetzt. Das sind alle Positionen der Lücken B.
Bei der Stapelung der gefalteten Schichten ändert sich demnach mit jeder Schicht die Neigung der trigonalen Prismen und gleichzeitig die Lückenbesetzung der C-Atome abwechselnd in die Positionen A oder B. Während die einzelnen Schichten der Fe-Atome allein völlig identisch sind, unterscheiden sie sich im Teilchenverband durch die Belegung mit C-Atomen. Von der Anzahl der Teilchen aus betrachtet ist es aber völlig gleichgültig, ob nur die Positionen A oder nur die Positionen B besetzt sind. Insofern muß bereits eine mit C-Atomen bestückte Schicht der Fe-Atome das erwartete Teilchenzahlenverhältnis von Eisen- zu Kohlenstoff-Atomen beinhalten.
Der in Abbildung 5.55 gekennzeichnete Ausschnitt E der gefalteten Schicht überspannt ein Tal von Kamm zu Kamm, auf den Kämmen wird er von zwei benachbarten Kammkugeln begrenzt. Dieser Ausschnitt bietet als Elementarzelle in der Ebene eine von mehreren Möglichkeiten, durch fortwährende, gleichmäßige Verschiebung in beiden Richtungen die gesamte Schicht zu beschreiben. Durch Abzählen der Teilchen innerhalb dieses zweidimensionalen Ausschnittes erhält man bereits das Teilchenzahlenverhältnis im Zementitkristall, das Summensymbol Fe6C2 bzw. Fe3C :
| Fe-Atome | 4 * 1/4 = 1 | C-Atome | 2 * 1/2 = 1 | ||
| 4 * 1/2 = 2 | 1 * 1/1 = 1 | ||||
| 3 * 1/1 = 3 | |||||
| ∑ 6 | ∑ 2 |
Den Ausschnitt E (vgl. Abb. 5.55) können wir verwenden, um eine dreidimensionale Elementarzelle aus den gestapelten Schichten herauszuschneiden, die den periodischen Aufbau der Zementitstruktur räumlich übersichtlich wiedergibt. Zur Grundfläche von E gehören nur die vier Eckkugeln in den Kammlagen. Schneiden wir waagerecht durch die Mittelpunkte dieser Kugeln und senkrecht durch die Kugeln auf den Seitenflächen bis zur übernächsten identischen Schicht, so bilden die Schnittebenen einen Quader der gesamten Kugelanordnung, den Abbildung 5.56 zeigt. Allerdings ist der Quader in der Darstellung sehr stark nach oben gestreckt, damit die verschiedenen Schichten besser zur Geltung kommen.
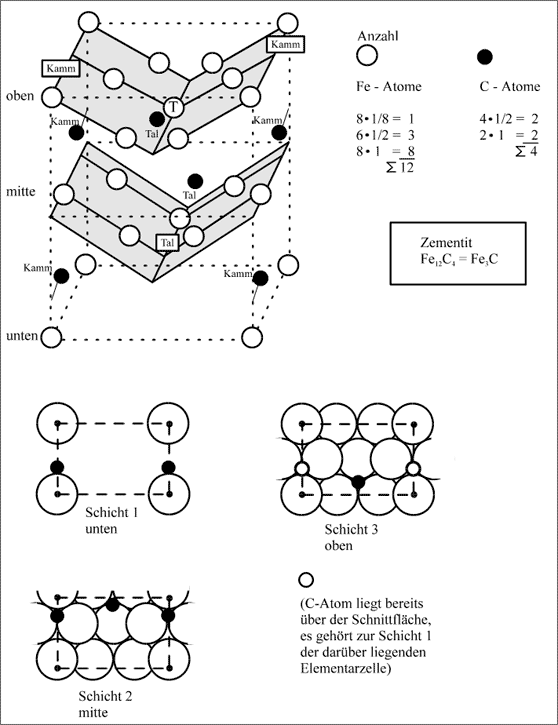
Abbildung 5.56: Die Elementarzelle des Zementit![]()
Die obere Schicht entspricht der unteren, insofern eine als mit unserem Muster des Ausschnittes E verglichen wird (vgl. Abb. 5.55). Die vier Fe-Atome als Kammkugeln bilden die Eckpunkte der Deckfläche, deren zwei Seiten von Kämmen gebildet werden. Zur Mitte zu verlaufen zwei gefaltete Flächen, die sich im Tal unter einem Winkel von 112° treffen. In der Mitte des Tales liegt die Kugel T. Anhand der Eckkugeln und der Kugel T kann man das Muster des Ausschnittes E unter Berücksichtigung der verschiedenen Höhenlagen auf die geknickte Fläche der oberen Schicht übertragen. Die mittlere Schicht ist identisch, aber um etwa ein Viertel des Abstandes von Kammkugel zu Kammkugel nach rückwärts verschoben. Dadurch geraten die Kugeln der Vorderfläche der Deckschicht ins Innere der Zelle, die der Rückseite wandern in die Nachbarzelle und zählen in unserem gewählten Ausschnitt nicht.
Die C-Atome muß man zwischen die Fe-Atome hineinmeditieren, dazu berücksichtigt man die Relativverschiebungen der Flächen gegeneinander. Hält man die obere Schicht fest und schiebt die untere Schicht zurück, dann ist es dasselbe, als wenn man die untere Schicht festhält und die obere Schicht nach vorne schiebt. Abbildung 5.56 zeigt zur Kontrolle die drei Schichten der Zelle mit der Besetzung in der Draufsicht. Das Abzählen der Teilchen innerhalb der Elementarzelle ist der Abbildung zu entnehmen: sie enthält 12 Fe-Atome und 4 C-Atome, was wiederum durch das Summensysmbol Fe3C ausgedrückt wird.
Wie schon mehrmals betont, sind die Fe-Atome durch das Falten der Schichten nicht mehr dichtest gepackt. Aber infolge der gleichzeitigen Bildung der trigonalen Prismen ist eine maximale Aufnahme von C-Atomen in das Eisengitter möglich: Alle trigonalen Prismenlücken werden mit C-Atomen besetzt. Im γ-Eisen dagegen sind die Oktaederlücken für diese Menge an C-Atomen zu klein, denn eine Oktaederlücke aus Fe-Atomen muß sich erheblich dehnen, um ein C-Atom beherbergen zu können. Das läßt das γ-Eisengitter nur zu, wenn nicht mehr als etwa 10% der Oktaederlücken besetzt werden.
Wenn die Zementitpackung nicht mehr dichtest gepackt ist, darf die Koordinationszahl der Fe-Atome nicht mehr 12 sein, sie muß sich ändern, wenn man die dichtest gepackten Schichten faltet. Wie groß ist sie ?
Die Auswirkung der Faltung auf die Koordinationszahl ist aber nicht auf alle Teilchen gleich, sondern hängt von deren spezieller Lage im Kugelverband ab: sie ist für Teilchen in der Kamm- und Tallage 12 (Höhen 1 und 4), die der anderen Teilchen lautet 11 (Höhen 2 und 3).
Dies können wir zunächst bei den Tal- und Kammteilchen verfolgen (vgl. Abb. 5.57). (a) zeigt aus einer Schicht eine Sechseckmasche des Kammes mit einem ausgewählten Teilchen A in seiner Koordination 6 - die zum Teil etwas aufgeweiteten Abstände spielen keine wichtige Rolle. Die Numerierung der Teilchen erlaubt deren Zuordnung zu drei verschiedenen Sechseckmaschen, die in (b) gestapelt sind. Die Stapelung mit der Abfolge ABAB der Sechserringe erfolgt auf den Kämmen und in den Tälern mit einer Verschiebung in Kamm- oder Talrichtung. Von vorn gesehen ist Teilchen A bezogen auf seine Umgebung mit den Teilchen 1 und 15 identisch, von oben gesehen ist das Teilchen 15 mit dem Teilchen 1 deckungsgleich, während das Teilchen A um etwa einen Kugelradius nach hinten gerückt ist.
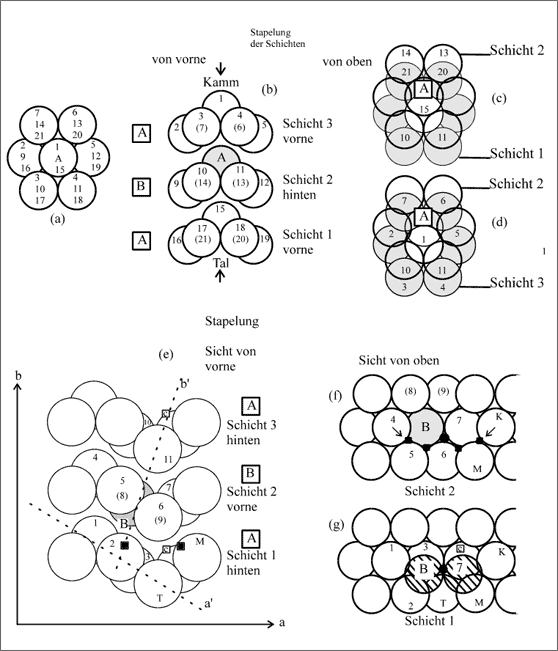
Abbildung 5.57: Veranschaulichung der Koordinationszahlen von Fe-Atomen im Zementgitter![]()
Wenn Schicht (a) als zweite Schicht nach hinten verschoben über der Schicht 1 zu liegen kommt, rastet das Teilchen 15 in die Lücke der Dreiecksmasche A,10,11 ein und gibt als einziges Teilchen einen Berührungspunkt der unteren Schicht zu Teilchen A. Die Teilchen 20 und 21 liegen für eine Berührung zum Teilchen A zu tief. Teilchen 15, 20, 21 in der unteren Schicht und Teilchen A,13,14 der oberen Schicht bilden zusammen die trigonale Prismalücke. Bei der Betrachtung der Projektionen der Teilchen senkrecht auf die Schichtebene ist immer zu berücksichtigen, daß alle Dreiecksmaschen erheblich geneigt sind und die trigonalen Prismen in Schräglage nach unten abgebildet werden.
In der Schicht 2 sitzt das Teilchen A erhaben zwischen seinen sechs Nachbarn, numeriert von 9-14, wobei die Teilchen 13 und 14 von vorne durch die Teilchen 11 und 10 verdeckt werden (b). Die Lage der Schicht 3 auf Schicht 2 wird durch (d) wiedergegeben. Ohne Anweisung für den Betrachter ist sie zunächst formal mit (c) identisch. Der entscheidende Unterschied liegt in der Zuordnung der Höhen der ein-zelnen Schichten. Während in (c) die stark umrandete Schicht 2 über der schraffierten Schicht 1 liegt, muß man dies in (d) umgekehrt sehen. Das Teilchen A wird dann von oben nur von den Teilchen 1,2,5,6,7 berührt, nicht jedoch von den Teilchen 3 und 4. Diese sind bereits zu weit vom Teilchen A abgerückt. Die Teilchen 1,3,4 der oberen Schicht 3 bilden zusammen mit den Teilchen A, 10 und 11 der unteren Schicht 2 das trigonale Prisma.
Zusammengenommen summiert sich die räumliche Koordinationszahl um das Teilchen A aus den Schichten 1,2 und 3 zu 1 + 6 + 5 = 12. Obwohl in der abgeknickten Kugelpackung bei den Kamm- und Talteilchen die räumliche Koordinationszahl mit der dichtesten Packung gleich ist, ist die Anordnung jedoch verschieden.
Zur Ermittlung der räumlichen Koordinationszahl der seitlich auf den Knickflächen gelegenen Teilchen B in den Höhen 2 und 3 betrachten wir (d) bis (g) der Abbildung 5.57. Die Stapelung der Schichten von vorn gesehen in der Folge ABAB zeigt (e), die Richtung der Schichten gibt die Achse a an, die Richtung der Stapelung die Achse b. Die Neigung der gefalteten Flächen ist durch die Achse a' beschrieben, auf der die Sechseckmaschen der Faltfläche senkrecht gestapelt sind.Würde man die drei abgebildeten Schichten ineinander einrasten lassen, dann wäre die Achse b' senkrecht zu a'. Die mittlere Schicht 2 soll um etwa einen Kugelradius nach vorne gezogen sein, die obere und untere Schicht sind nach hinten verlagert.
Die Ansicht der mittleren Schicht 2 von oben gesehen (f) macht deutlich, daß das ausgewählte Teilchen B von sechs Nachbarteilchen eingebunden ist. Von oben kaum ersichtlich ist, daß die Teilchen 4,5,6,8,9 mit dem Teilchen B zusammen in einer Ebene liegen, nur das Teilchen 7 weicht nach oben aus. Dies ist jedoch anhand der Figur (e) bei der zweiten Schicht gut erkennbar, wobei die Teilchen 8 und 9 von den Teilchen 5 und 6 verdeckt werden. Die Schicht 2 rastet in die Schicht 1 so ein, daß das Teilchen B in die Lücke 1,2,3 der unteren Schicht 1 zu liegen kommt und das Teilchen 7 in die Lücke C,M,K (g). Diese beiden Lücken liegen auf den beiden gefalteten Seitenflächen. In (f) sind die beiden analogen Lücken durch kleine Pfeile gekennzeichnet.
Die Projektion senkrecht nach unten (g) täuscht die beiden Lücken T,2,3 und T,M,C als bevorzugt vor. Sie liegen jedoch zu tief neben der Lücke im Tal, die ein C-Atom aufnehmen könnte. Das Teilchen B wird demnach wie in einer dichtesten Kugelpackung von drei Teilchen der unteren Schicht berührt. Die dritte Schicht wird auf die zweite in Art der hexagonal dichtesten Kugelpackung gestapelt, wobei als Bezugsebene die Faltfläche mit der Neigung a' herangezogen wird. Den drei Teilchen 1, 2 und 3 der Grundfläche würden in der Schicht 3, der Deckfläche, die Teilchen 10, 11 und C entsprechen. Das Teilchen C liegt aber höher und nicht mehr in der geneigten Faltfläche wie die Teilchen 10 und 11. Insofern wird das Teilchen B der zweiten Schicht von der oberen Schicht nur noch von den Teilchen 10 und 11 berührt. Räumlich wird das Teilchen B demnach von der unteren Schicht durch drei, in der eigenen Schicht von 6 und von der oberen von zwei Teilchen, also insgesamt von elf Teilchen berührend umgeben. Das ist ein Teilchen weniger als in einer dichtesten Kugelpackung.
Schließlich stellt sich die Frage, in welchem Verhältnis die Kamm- und Talteilchen A zu den Seitenteilchen B in der gefalteten Kugelanordnung vorhanden sind. Das beantwortet ein Blick auf Abbildung 5.55: eine Kugelschicht muß bereits das Verhältnis der Teilchen wie im ganzen Stapelhaufen zeigen. Im gekennzeichneten Bereich E schneiden wir aus:
| Kamm- und Talteilchen | Seitenteilchen | ||||
| 4 * 1/4 = 1 | 4 * 1/2 = 2 | ||||
| 1 * 1/1 = 1 | 2 * 1/1 = 2 | ||||
| 2 | 4 | = 6 |
Von sechs Fe-Atomen besitzen immer zwei die räumliche Koordinationszahl 12 und vier die Koordinationszahl 11. Daraus können wir eine durchschnittliche Koordina-tionszahl errechen:
2 * 12 + 4 * 11 = 68
Durchschnittlich werden also sechs Teilchen insgesamt von 68 Teilchen umgeben, die durchschnittliche Koordinationszahl eines Fe-Teilchens beträgt daher 11,33. Das zeigt, daß die Fe-Atome durch das Falten der Schichten nicht mehr dichtest gepackt sind.
Eine Zusammenfassung aller bisher skizzierten Strukturen von Legierungen zeigt abschließend Abbildung 5.58. Im nächsten Abschnitt sollen weitere, allgemeine Eigenschaften von Legierungen diskutiert werden.
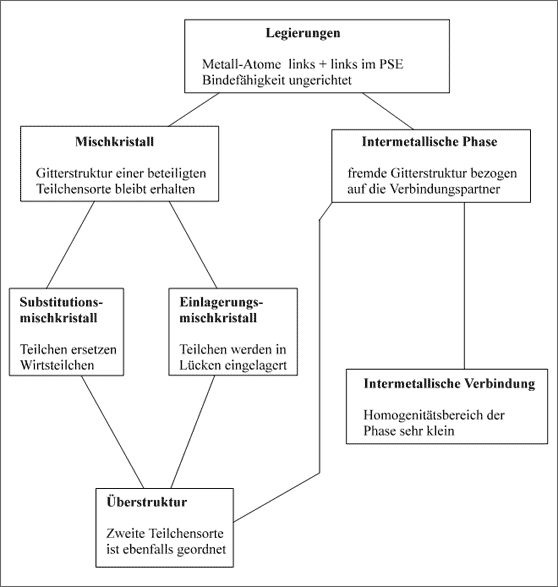
Abbildung 5.58: Übersicht über verschiedene Klassen von Legierungen
![]()


