5.2.3.1 Substitutionsmischkristalle
Einen Substitutionsmischkristall stellen wir uns zunächst als fertiges Gitter der Muttersubstanz vor, dem wir einzelne Teilchen entnehmen und deren Plätze wir durch andere Teilchen besetzen. Maßgebend sind natürlich Größe und Bindekräfte der beteiligten Teilchen. Im folgenden werden wir drei markante Fälle dieser Teilchenkombinationen durchspielen. Diese Fälle sind typisch und häufig anzutreffen, sie sollen uns vom Einfachen zum Komplizierten führen.
1. Lückenlose Mischkristallreihe. Der einfachste Fall ist der, daß sich die substituierten Teilchen ebenso verhalten wie die Teilchen des Mutterkristalls. Dann dürfte es keine Schwierigkeiten bereiten, in der Modellvorstellung von weißen und schwarzen Kugeln eine weiße Kugel nach der anderen auszutauschen, bis zuletzt eine reine schwarze Kugelpackung entstanden ist.
Was bedeutet es aber, daß ein Teilchen in seinen Eigenschaften völlig denen eines anderen Teilchens gleicht ? Ein Teilchen, das sich bei der Substitution wie ein Teilchen des Wirtsgitters verhält, muß die
a) gleiche Größe aufweisen,
b) gleichen Bindekräfte besitzen,
c) gleiche Gitterstruktur aufbauen.
Größe der Teilchen. In der Praxis werden im allgemeinen vom Wirtsgitter noch Abweichungen des Atomradius bis ca. 15 % hingenommen. Die "Welligkeit" der Teilchenschichten wird durch langsam fortschreitendes Dehnen oder Schrumpfen des Gitters ausgeglichen. Bei einer Abweichung der Atomradien von über 15 % ist allerdings mit einer Substitution nicht mehr zu rechnen.
Bindekräfte. Die Stärke der Bindekräfte beider beteiligter Teilchenarten muß etwa gleich groß sein. Offensichtlich werden auch hier Abweichungen vom Wirtsgitter geduldet, die aber nicht in Zahlen zu fassen sind: letztlich entscheidet das Experiment. Nicht nur die Stärke der Kräfte muß gleich sein, selbstverständlich auch die Art der ungerichteten Bindekräfte: Gerichtete Bindungsanteile der substituierenden Teilchensorte über ein bestimmtes Maß hinaus lassen keine gemeinsame Struktur bei der Substitution zu.
Gitterstruktur. Sollen lediglich durch Substitution die Teilchen der Muttersubstanz durch andere Teilchen im Gitter ersetzt werden, so bleibt zwingend die Art der Gitterstruktur erhalten. Bilden die weißen Teilchen der Muttersubstanz modellmäßig eine kubisch dichteste Kugelpackung und stellen wir uns für die substituierenden schwarzen Teilchen vor, daß sie eine hexagonale Struktur aufbauen, so wäre ein kontinuierlicher Austausch unmöglich. Was die Teilchen tun, wenn man dieses Manöver trotzdem probiert, darüber mehr in den folgenden Abschnitten.
Suchen wir nach einem Teilchenpaar, das dem beschriebenen Idealverhalten möglichst nahe kommt, vergleichen wir beispielsweise Kupfer-, Silber- und Gold-Atome.
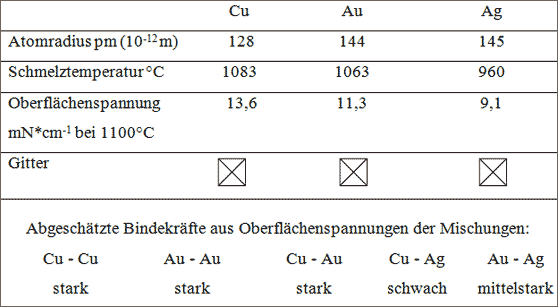
Tabelle 5.9: Vergleich von Kupfer-, Silber- und Gold-Atomen bezüglich der Möglichkeiten zur Substitution (vgl. Abb. 5.31)
Beispiel Kupfer - Gold. Der Vergleich aus Tabelle 5.9 läßt folgende Schlüsse zu:
a) Die Differenz der Atomradien beträgt auf das Gold-Atom bezogen11 %: das ist erfahrungsgemäß zur Mischkristallbildung gerade noch tragbar,
b) die übereinstimmenden Schmelztemperaturen und Oberflächenspannungen der reinen Schmelzen lassen auf ähnliche Bindekräfte der Teilchenarten schließen,
c) beide Teilchenarten bauen allein für sich das kubisch flächenzentrierte Gitter.
Die Voraussetzungen zum Bau von Mischkristallen in der Art, daß ausgehend vom Kupfer alle Cu-Atome kontinuierlich gegen Au-Atome ausgetauscht werden, sind gut. Das wird durch das Experiment bestätigt. Im Labor ist durch Zusammenschmelzen von Kupfer und Gold jeder beliebige Mischkristall herstellbar. Dabei wechselt die Kupferfarbe ganz allmählich zur Goldfarbe. Ein hoher Anteil an Kupfer gibt zum Beispiel Rotgold seinen Namen. Neben der Farbe ändern sich ebenfalls andere physikalische Eigenschaften wie Härte oder elektrische Leitfähigkeit von Mischkristall zu Mischkristall. Da reines Gold sehr weich ist, wird für Münzzwecke etwa 10 % Kupfer dazulegiert. Die fertige Münze besteht dann aus vielen feinen Gold-Kupfer-Mischkristallen.
Beispiel Gold - Silber. Aus den gleichen Gründen wie zuvor scheinen die Vor-aussetzungen zum Bau von beliebigen Au-Ag-Mischkristallen günstig zu sein. Das Experiment läßt tatsächlich jeden beliebigen Mischkristall durch Zusammenschmelzen von Gold und Silber zu. Diese Mischkristalle sind beliebte Werkstoffe für die Goldschmuckindustrie.
Das Beispiel Kupfer - Silber. Auch in diesem Beispiel sind die Unterschiede bei den Atomradien und Schmelztemperaturen noch tragbar. Allerdings weichen die Oberflächenspannungen sehr voneinander ab, so daß Unterschiede in den Bindungsstärken beider Teilchenarten vorhanden sein müssen.Die Oberflächenspannungen der Mischungen lassen darüber hinaus zu wünschen übrig und deuten auf sehr schlechte Bindekräfte zwischen Cu- und Ag-Atomen hin. Die Voraussetzungen zur Bildung von Mischkristallen beliebiger Zusammensetzung sind deshalb nicht gut. Das Experiment bestätigt diese Vermutung: Cu- und Ag-Atome sind zwar zu Mischkristallen zusammensetzbar, aber nicht in der beliebigen Weise wie bei Au/Ag- oder Au/Cu-Mischkristallen.
Mischkristallreihen. Die Möglichkeiten der Teilchenkombinationen sind auf jeden Fall immer im Experiment zu prüfen. Die Teilchen werden in den verschiedenen Zahlenverhältnissen zusammengegeben und meistens in der Schmelze miteinander gemischt, durch den Wärmeentzug bei einer bestimmten Temperatur setzen sie sich dann zusammen. Der Metallograph prüft, auf welche Weise sie sich verknüpft haben, und gibt die Meßergebnisse in einem speziellen Protokoll als Information weiter.
In unserem Fall der Kombinationsmöglichkeit von Gold und Silber wurde bei jedem Teilchenverhältnis ein Mischkristall mit kubisch flächenzentriertem Gitter gemessen. Zur Verdeutlichung sind einige dieser Kristalle in Abhängigkeit von der Konzentration im Modell gezeichnet worden (vgl. (1) in Abb. 5.35).
Man nennt dies eine Mischkristallreihe über den gesamten Konzentrationsbereich. Auch jeder andere Mischkristall, der hier konzentrationsmäßig nicht angegeben ist, zeigt das gleiche Ergebnis: Au- und Ag-Atome weisen dementsprechend eine lückenlose Mischkristallreihe auf. Lückenlos bedeutet also hier: für jede beliebige Konzentration existiert ein Mischkristall. Das normale Meßprotokoll ist hier nicht sonderlich aufwendig - es genügt letztlich eine Gerade, auf der die Konzentration der beiden Substanzen gegenläufig aufgetragen ist. Dazu wird die Kristallstruktur angegeben (2).
Des besseren Aussehens wegen wird die Konzentrationsgerade meistens als Band dargestellt, das sich besser überblicken läßt. Außerdem wird häufig die Konzentrationsangabe der zweiten Teilchenart, der zweiten "Komponente", weggelassen, da sie jeder selbst durch Ergänzen auf 100 leicht berechnen kann (3).
Als weitere Beispiele für lückenlose Mischkristallreihen mit kubisch flächenzentriertem Gitter seien hier erwähnt: Cu/Au, Cu/Ni, γ-Fe/Pt, γ-Fe/Ni. Beispiele für lückenlose Mischkristallreihen des kubisch raumzentrierten Gitters sind: Mo/W, α-Fe/V, α-Fe/Cr. Beispiel für eine lückenlose Mischkristallreihe mit hexagonal dichtester Struktur: Mg/Cd.
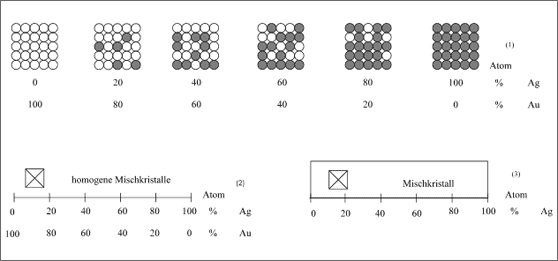
Abbildung 5.35: Modellvorstellungen zur Au-Ag-Mischkristallreihe
Kupfer-Nickel-Mischkristalle sind nicht nur bemerkenswert wegen ihrer sehr guten korrosionsbeständigen Eigenschaften oder der Verwendung als Widerstandsdraht (Konstantan), sondern sie sind auch merkenswert, da sie jeder von uns fast alltäglich in die Hand nimmt. Unsere silberfarben aussehenden Münzen (0,50 DM bis 5,00 DM) bestehen aus Mischkristallen von 75 % Cu und 25 % Ni. Dieser Angabe in Massenprozent entsprechen 73 Atom% Cu und 27 Atom % Ni.
Beim Mischkristall γ-Fe/Ni ist zu beachten, daß reines γ-Fe nur bei hohen Temperaturen beständig ist. Durch die Wechselwirkung der Kräfte bei der Fe/Ni-Mischkristallbildung ändert sich jedoch der Temperaturbereich, in dem γ-Fe stabil ist. Fe/Ni-Legierungen sind als Edelstähle gut bekannt.
Streng genommen stellt nun jeder Mischkristall einer Mischkristallreihe mit etwas anderer Zusammensetzung jeweils eine andere Substanz dar. Die Eigenschaften dieser unendlich vielen Substanzen ändern sich jedoch völlig kontinuierlich mit der Konzentration, so daß das Problem der eindeutigen Substanz in eine philosophische Frage übergeht, beispielsweise in die berühmte Frage der griechischen Philosophen: „Wie viele Körner Reis machen einen Reishaufen“?
Im allgemeinen gibt man deshalb die Konzentrationen bei den Materialien mit an und besitzt damit eine eindeutige Informationsmöglichkeit.
2. Begrenzte Mischkristallbildung. Die lückenlose Mischkristallbildung ist zu verstehen, wenn vorausgesetzt wird, daß sich beide Teilchenarten gleich verhalten. In der Praxis ist das allerdings selten der Fall. Viel häufiger unterscheiden sich die Teilchen in folgender Weise:
a) Die Teilchenradien sind zu unterschiedlich,
b) die Bindekräfte zwischen den unterschiedlichen Teilchensorten sind sehr klein,
c) die Teilchenarten bilden je ein anderes Wirtsgitter.
Beispiel Kupfer - Silber. Es ist zwar trotzdem in vielen Fällen möglich, daß sich Mischkristalle bilden, aber nicht in jedem beliebigen Teilchenverhältnis. Betrachten wir zuerst das Teilchen-Paar Cu-Ag. Alle Voraussetzungen für eine lückenlose Mischkristallreihe würden bestehen, wenn die Cu-Ag-Bindekräfte nicht sehr schwach wären. Wahrscheinlich werden die Cu-Atome untereinander am stärksten gebunden: Sie setzen sich aufgrund ihrer starken Bindekräfte zuerst zusammen und bauen einige Ag-Atome in den Mischkristall ein (bis zu etwa 4 Atom% Ag). Ebenso bilden die Ag-Atome einen eigenen Mischkristall, in den einige Cu-Atome eingebaut vorliegen (bis zu etwa 12 Atom% Cu). Es existieren zwischen Kupfer und Silber demnach zwei Mischkristallsorten, eine reich an Kupfer, die andere reich an Silber.
Die protokollarische Darstellung des Meßergebnisses aus dem Labor zeigt (a) in Abbildung 5.36. Gedanklich dulden demnach 96 Cu-Atome maximal etwa 4 Ag-Atome in ihrem Gitter. Wiederum können 88 Ag-Atome nur maximal 12 Cu-Atome in das Kristallgitter aufnehmen, d. h. 12 von 100 Ag-Atomen stellen ihre Plätze für Cu-Atome in ihrem kubisch flächenzentrierten Gitter zur Verfügung. Selbstverständlich können die Kupfermischkristalle auch weniger als 4 Atom% Ag einbauen und die Silbermischkristalle weniger als 12 Atom% Cu. Dies ist deutlich im Konzentrationsband durch die Markierung der Bandflächen bis 4 Atom% Ag bzw. 12 Atom% Cu zu erkennen (vgl. Abb. 5.36). Allerdings existieren keine anderen Mischkristallsorten. Einen Cu/Ag-Mischkristall mit 60 Atom% Ag und 40 Atom% Cu gibt es eben nicht, da sich ja die jeweiligen Atomarten hauptsächlich selbst verknüpfen. Zwischen 4 und 88 Atom% Ag, bzw. 96 und 12 Atom% Cu tritt eine Lücke in der Mischkristallbildung auf. Diese Lücke ist auf dem Konzentrationsband der Abbildung 5.36 ersichtlich.
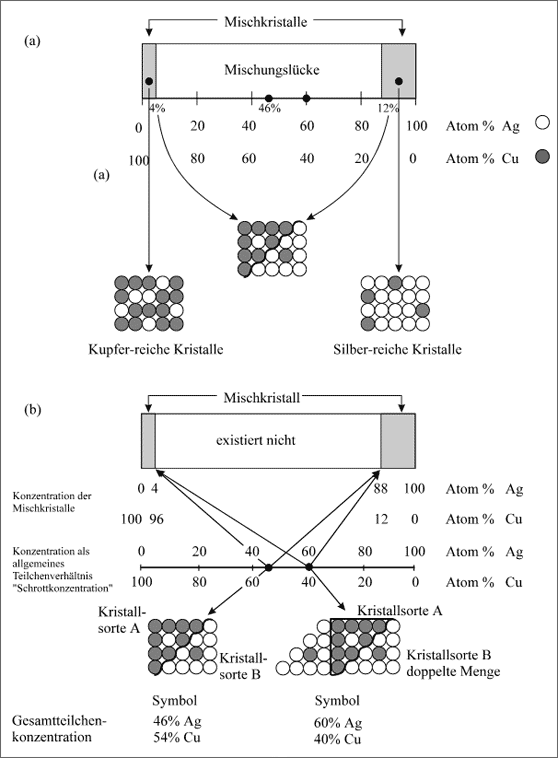
Abbildung 5.36: Modellvorstellungen zur Cu/Ag-Mischkristallreihe
Da in früheren Zeiten die Mischkristallbildung noch nicht so richtig durchschaubar war, hat man statt vom Teilchenzusammensetzen einfach vom "Mischen" gesprochen. Das geht darauf zurück, daß man die Schmelzen gemischt und die Mischung abgekühlt hat. Auf jeden Fall ist das Wort "Mischung" in dem Ausdruck "Mischungslücke" als In-formation letztlich für "einheitliches Zusammensetzen" geblieben. Die Mischungslücke bezeichnet einen Konzentrationsbereich, in dem sich die Teilchen in einem daraus ausgewählten Zahlenverhältnis nicht zu einem einheitlichen, homogenen Kristall zusammensetzen.
Wie sinnvoll ist es dann aber, auf dem Konzentrationsband die Werte 46 bzw. 60 Atom% Ag anzugeben? Mischkristalle dieser Konzentrationen gibt es jedenfalls nicht. Eine Angabe des Teilchenzahlenverhältnisses für etwas, das es nicht gibt, ist allerdings unsinnig. Nun existieren aber sicherlich Schmelzen der angegebenen Konzentrationen, oder auch Silber-Kupfer-Schrott mag gerade die Zusammensetzung 60 Atom% Ag haben. Es sind allgemeine Konzentrationsangaben, die keine Aussagen über die Existenz von Mischkristallen machen. Deshalb ist es am Anfang hilfreich, eine zweite Koordinate einzuführen, die lediglich allgemeine Konzentrationen oder "Schrottkonzentrationen" angibt. Die erste Koordinate kann daraufhin genauer mit "Konzentration der Mischkristalle" bezeichnet werden. Beide Bezeichnungen sind in (b) der Abbildung 5.36 zu finden. Man erkennt nun mit der Trennung beider Konzentrationsachsen und der Angabe von Pfeilen deutlicher, daß beim Abkühlen von Schmelzen der Schrottkonzentrationen 46 oder 60 Atom% Ag die Mischkristalle mit jeweils 4 und 88 Atom% Ag entstehen und und zu heterogenen Kristallen zusammenwachsen.
Um diesen Sachverhalt noch anschaulicher zu machen, führen wir folgendes Gedan-kenexperiment durch - wohl wissend, daß bei 46 Atom% Ag ein Mischkristall nicht existiert. Wir geben trotzdem eine entsprechende Anzahl Ag-Modellkugeln und Cu-Modellkugeln in einen gedachten Topf und verfolgen das modellmäßige Zusammen-setzen dieser Kugeln zu Kristallen (vgl. Tab. 5.10).
Stellen wir uns vor, 108 Cu-Atome und 92 Ag-Atome bewegen sich frei in unserem Topf, bis wir durch Wärmeentzug, also Verkleinerung der Wärmebewegung, das Signal zum Zusammensetzen geben. Die Gesamtkonzentration unserer Teilchen beträgt 46 Atom% Ag und 54 Atom% Cu (vgl. Tab. 5.10). Was werden die Teilchen tun? Einen einheitlichen, homogenen Kristall dieser Konzentration gibt es nicht. Es werden sich demnach 96 Cu-Atome mit 4 Ag-Atomen zu einem einheitlichen Kristall zusam-mensetzen und ebenso die 88 Ag-Atome mit 12 Cu-Atomen. Wir erhalten von jeder der beiden Kristallsorten einen homogenen Mischkristall. Diese Kristalle verknüpfen sich zu einem heterogenen Kristallsystem (vgl. Abb. 5.36). Überlegen wir uns ein zweiteses Beispiel. Von 300 frei beweglichen Teilchen in einem Topf sind 120 Cu-Atome und 180 Ag-Atome, das sind 40 Atom% Cu und 60 Atom% Ag. Wie setzten sich diese Teilchen zusammen? 96 Cu-Atome nehmen wieder 4 Ag-Atome mit in ihr Gitter auf. Die restlichen 176 Ag-Atome verknüpfen sich mit 24 Cu-Atomen zum anderen Mischkristall, der doppelt so groß ist, wie der Kristall im ersten Beispiel.
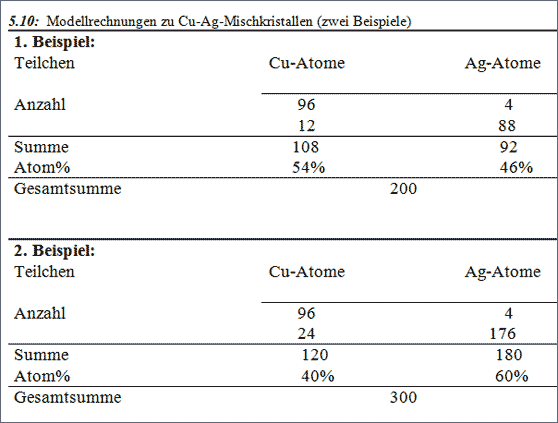
5.10: Modellrechnungen zu Cu-Ag-Mischkristallen (zwei Beispiele)
Wir erhalten also wieder die zwei Mischkristallsorten, den Cu-Mischkristall mit 4 Atom% Ag und den Ag-Mischkristall mit 12 Atom% Cu. Gemeinsam bilden sie einen heterogenen Mischkristall. Je größer in einem Topf das Angebot an Ag-Atomen im Verhältnis zu den Cu-Atomen ist, desto mehr Kristalle der Ag-Mischkristallsorte werden entstehen und desto weniger der Cu-Mischkristallsorte. Bei 88 Atom% Ag wird dann nur mehr die Kristallsorte des Ag-Mischkristalls mit 12 Atom% Cu gebildet.
Heterogene Kristalle. Für ein heterogenes System von Kristallen, das aus zwei Kristallsorten von jeweils zwei gleichen Teilchenarten besteht, sind zur Beschreibung drei Größen geläufig, die streng unterschieden werden müssen:
1. Konzentrationen in beiden Kristallsorten,
2. Menge der verschiedenen Kristallsorten,
3. Gesamtkonzentration der beiden Teilchenarten.
Das folgende Modellbeispiel (vgl. Abb. 5.37) soll die einzelnen Größen übersichtlich herausstellen: Je 10 Teilchen bilden einen kleinen Kristallit. Die Struktur aller Kristallite soll gleich sein. 10 solcher Kristallite bilden den Gesamtkristall, er besteht somit insgesamt aus 100 Teilchen.
Von den 100 Teilchen seien 64 weiß und 36 schwarz. Die Konzentration der Teilchen in den Kristalliten sei unterschiedlich: Es existieren zwei Kristallsorten. Die eine Kristallsorte A enthält 6 schwarze und 4 weiße Teilchen, die andere Kristallsorte B enthält 3 schwarze und 7 weiße Teilchen. Von der Kristallsorte A sind dementsprechend zwei Kristalle, von der Sorte B acht Kristalle vorhanden. Somit ergeben sich folgende Überlegungen:
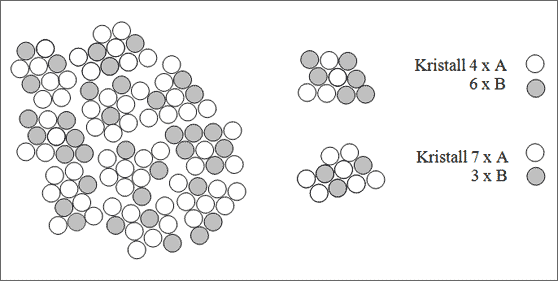
Abbildung 5.37: Modell eines heterogenen Mischkristalls
1. Teilchen-Konzentrationen in beiden Kristallsorten
Kristallsorte A: 40 % weiß, 60 % schwarz
Kristallsorte B: 70 % weiß, 30 % schwarz
2. Menge der verschiedenen Kristallsorten
Anzahl aller Kristalle: A + B = 10
davon: 2 x A = 20 % A, 8 x B = 80 % B
3. Gesamtkonzentrationen
64 Teilchen weiß von 100: 64 Teilchen%
36 Teilchen schwarz von 100: 36 Teilchen%
Beispiel Zink - Magnesium. Wir haben bisher das Phänomen der begrenzten Mischkristallbildung am Teilchenpaar Cu/Ag erläutert, wobei die Ursache der Begrenzung durch die geringe Bindekraft zwischen Cu- und Ag-Atomen gedeutet wurde. Ein Beispiel für begrenzte Mischkristallbildung infolge unterschiedlicher Atomradien ist das Paar Zn/Mg. Der Radius für ein Mg-Atom beträgt 160 pm, für ein Zn-Atom 133 pm. Das ergibt eine Abweichung von 20 %. Trotzdem können die großen Mg-Atome noch bis zu 3,3 Atom% Zn einbauen, allerdings die kleinen Zn-Atome in ihren Verband maximal nur 0,4 Atom% Mg. Das Verhalten können wir wiederum mit einem Konzentrationsband darstellen (vgl. (a) in Abb. 5.38).
Beispiel Eisen - Nickel. Schließlich soll noch ein Teilchenpaar genannt werden, das eine Mischungslücke durch den unterschiedlichen Kristallgitterbau der beiden Teilchenarten bedingt: α-Fe/Ni (vgl. (b) in Abb. 5.38).
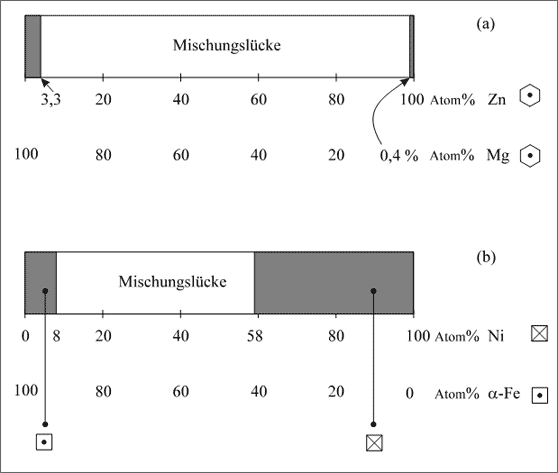
Abbildung 5.38: Mischkristallbildung an den Beispielen Zn/Mg und α-Fe/Ni
Nickel weist durchweg ein kubisch flächenzentriertes Gitter auf, wie es bei γ-Eisen oberhalb von 906 °C der Fall ist. In diesem Temperaturbereich bilden Nickel und Eisen tatsächlich eine lückenlose Mischkristallreihe. Bei niedrigen Temperaturen ist Eisen allerdings nur als α-Eisen mit kubisch raumzentriertem Gitter beständig. Es können aber auch hier Fe-Atome gegen Ni-Atome ausgetauscht werden, es entsteht ein kubisch raumzentrierter Substitutionsmischkristall. Die Grenze liegt bei etwa 8 % Ni-Atome, dann vereinigen sich weitere Ni-Atome und bauen einen Kristall mit bis zu 58 % Ni-Atomen im kubisch flächenzentrierten Gitter. Dieser Mischkristall enthält dann maximal 42 Atom% Fe (vgl. (b) in Abb. 5.38).
Bildung nur einer Mischkristallsorte. Wir wollen nun Fälle betrachten, wenn mehrere Voraussetzungen zur Mischkristallbildung sehr schlecht sind, trotzdem aber noch Mischkristalle auftreten. Als Beispiel diene das Paar Blei/Zinn. Die Radien sind 175 pm für das Pb-Atom, 150 pm für das Sn-Atom (Abweichung: 17 %).
Zinn besitzt ein außergewöhnliches Metallgitter, eine Art einfach gestrecktes Würfelgitter mit der Koordinationszahl 6. Es neigt bezüglich seiner Bindekräfte schon ganz leicht zu den Nichtmetallen mit erheblichen Anteilen gerichteter Binde-fähigkeiten und erinnert an die nichtmetallischen Verwandten im Periodensystem, an das Germanium und Silicium. Blei setzt sich dagegen aus Metall-Atomen mit völlig ungerichteten Bindekräften zusammen, das Metallgitter ist kubisch flächenzentriert mit der Koordinationszahl 12.
Sicher sind hier die Chancen zum Bau von Mischkristallen schlecht, und doch kann ein Bleikristall Pb-Atome gegen Sn-Atome austauschen, ca. bis 25 Atom% bei ungefähr 180 °C. Bei Zimmertemperatur sind es noch 4 Atom%. Das Zinn ist aber nicht in der Lage, Pb-Atome in sein Gitter aufzunehmen, es bildet keinen Mischkristall mit Blei (vgl. (a) in Abb. 5.39).

Abbildung 5.39: Mischkristallbildung an den Beispielen Pb/Sn und Pb/Zn
In diesem Konzentrationsband ist nur auf der rechten Seite die Existenz eines Mischkristalls angegeben und die linke Seite erscheint leer, es existieren lediglich 0 % Pb bzw. 100 % Zinn. Dies wird durch einen Punkt bei 100 % Zinn auf der Gerade bzw. durch einen senkrechten Strich am Anfang des Bandes signalisiert. Existenzbereiche in unserem Band sind also das schraffierte Mischkristallfeld auf der Blei-Seite und der Strich auf der Zinn-Seite! Gibt man nun gedanklich viele Sn- und Pb-Atome in einen Topf, dann werden sich hauptsächlich Pb-Atome mit einigen Sn-Atomen zum Mischkristall zusammen setzen, aber Sn-Atome nur untereinander zum reinen Zinnkristall verknüpfen.
Keine Mischkristallbildung. Hier fassen wir alle die Fälle zusammen, in denen durch ungünstige Radien-, Bindungs- und Gitterverhältnisse überhaupt keine Mischkristalle zustande kommen. Häufig ist an solchen Systemen das Blei beteiligt, weil es gegenüber den gängigen Metallen einen sehr großen Atomradius besitzt (175 pm). Einige Beispiele seien erläutert.
Blei/Aluminium. Das Pb-Atom ist um 22% größer als das Al-Atom. Beide Teilchenarten bauen zwar das gleiche kubisch flächenzentrierte Gitter, aber Al-Atome betätigten bereits erheblich gerichtete Bindekräfte.
Blei/Eisen. Das Pb-Atom ist um 41% größer als das Fe-Atom, die Gitterstrukturen stimmen nicht überein: Das Eisengitter ist bei Normaltemperatur kubisch raumzentriert, das Bleigitter aber kubisch flächenzentriert.
Blei/Zink. Das Pb-Atom ist um 32% größer als das Zn-Atom, außerdem bauen Pb-Atome eine kubisch dichteste und Zn-Atome eine hexagonal dichteste Kugelpackung dieses System weist ebenfalls eine völlige Mischungslücke auf (vgl. (b) in Abb. 5.39). Beim Abkühlen einer Blei-Zink-Schmelze werden sich also immer nur die Pb-Atome untereinander und die Zn-Atome untereinander zusammensetzen: Wir erhalten zwei Kristallsorten, die durch schwache Bindekräfte zusammenhalten. Diese beiden Kristallsorten sind die reinen Kristalle von Blei und Zink.
Die Mischungslücke im Konzentrationsband wird auch als Heterogenitätsbereich bezeichnet, im Gegensatz dazu wird der Bereich, in dem ein Kristall existieren kann, Homogenitätsbereich genannt.
Stellen wir unsere vier typischen Fälle der Mischkristallbildung anhand der Konzentrationsbänder nochmal gegenüber (vgl. Abb. 5.40):
1. Das System Cu/Ni besitzt einen lückenlosen Homogenitätsbereich von 0-100 %.
2. Das System Fe/Ni zeigt einen Homogenitätsbereich von 0-8 und von 58-100 Atom% Ni, dazwischen existiert ein Heterogenitätsbereich, eine Mischungslücke.
3. Das System Sn/Pb besitzt von 0-75 Atom% Pb einen Heterogenitätsbereich, eine Mischungslücke. Ein Homogenitätsbereich existiert nur von 75-100 Atom% Pb.
4. Für das System Zn/Pb existiert nur ein Heterogenitätsbereich, eine völlige Mischungslücke. Als homogene Phasen treten nur reines Blei und reines Zink auf.
3. Überstruktur. Bei einem Substitutionsmischkristall kann die fremde Teilchenart statistisch oder geordnet eingebaut sein. Die überwiegend auftretende Formation ist die statistische Verteilung, dies meist bei höheren Temperaturen. Aber trotzdem existiert eine ganze Reihe von Kristallen mit geordnetem Einbau der anderen Teilchenart, die dementsprechend auch andere Materialeigenschaften besitzen. Systeme dieser Art sind beispielsweise Cu/Au, Co/Fe, Ni/Fe oder Ni/Co. Wird die zweite Teilchenart geordnet im Kristall eingebaut, bezeichnet man dies mit dem Begriff Überstruktur. Als Beispiele seien zwei kubische Überstrukturen des lückenlosen Cu/Au-Mischkristallsystems vorgestellt (vgl. Abb. 5.41).
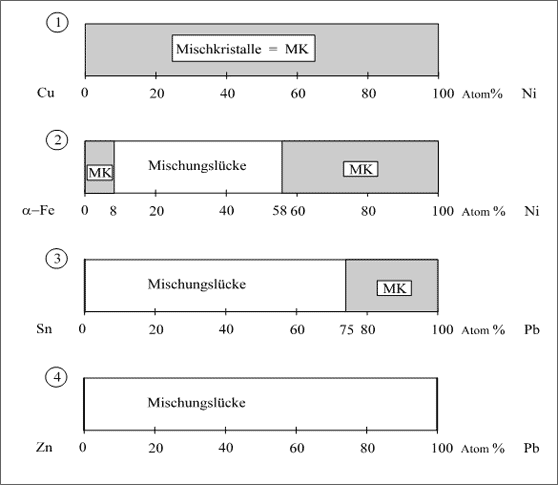
Abbildung 5.40: Vier typische Fälle der Mischkristallbildung
Das Modell (1) stellt eine Überstruktur dar, in der vom kubisch flächenzentrierten Elementarwürfel ausgehend vier Zentren einer Ebene mit Cu-Atomen besetzt sind, alle Würfelecken und die Zentren der Deckflächen aber durch Au-Atome. Geht man von Quadratmaschen aus, so folgt einer Schicht von Cu-Atomen jeweils eine von Au-Atomen und umgekehrt. Jedes Cu-Atom ist also von 4 weiteren Cu-Atomen und von 8 Au-Atomen umgeben, jedes Au-Atom von 4 weiteren Au-Atomen und 8 Cu-Atomen.
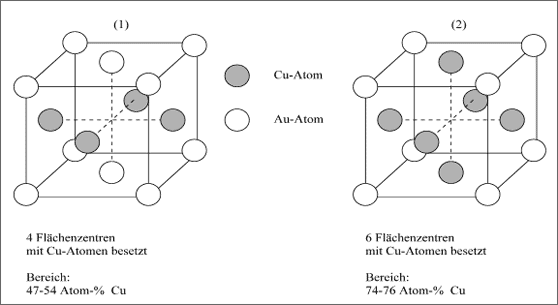
Abbildung 5.41: Cu/Au-Mischkristallbildung in Form zweier Überstrukturen
Die exakte Zusammensetzung verlangt ebenso viele Cu-Atome wie Au-Atome, also ein Zahlenverhältnis 1:1 oder Cu1Au1 bzw. CuAu. Selbst wenn es nicht ganz genau vorliegt, wird diese Überstruktur im Bereich von 47-54 Atom% Cu bevorzugt. Einige wenige gedachte Würfelzellen sind dann mit Cu-Atomen unter- oder überbesetzt.
Ein weiterer Überstruktur-Mischkristall (2) leitet sich aus dem ersten dadurch ab, daß im Elementarwürfel auch die Flächenzentren der Deckflächen mit Cu-Atomen besetzt sind: Einer Schicht von Cu-Atomen folgt jeweils eine Schicht, in der 50 % Cu-Atome und 50 % Au-Atome ein regelmäßiges Quadratmuster bilden. Dadurch ist dann jedes Au-Atom von 12 Cu-Atomen umgeben und jedes Cu-Atom von 4 Au-Atomen und 8 Cu-Atomen. Als exakte Zusammensetzung bedingt dies dreimal so viele Cu-Atome wie Au-Atome, also ein Atomzahlenverhältnis Cu : Au = 3:1. Es wird auch in Form der Symbole Cu3Au1 bzw Cu3Au ausgedrückt.
![]()


