5.1.6 Anzahl der Oktaeder und Tetraeder in einer dichtesten
Kugelpackung
Wir kennen die dichtesten Kugelpackungen jetzt bereits recht genau. Wir wissen etwas über den Aufbau, die Art der Hohlräume und deren Lage. Wir wissen aber noch nichts über die Anzahl der Lücken, die von einer vorgegebenen Kugelmenge gebaut werden. Wieviele Oktaeder- und Tetraederlücken entstehen, wenn wir z. B. 1000 Kugeln dichtest zusammensetzen? Diese Frage wird eine Rolle spielen, wenn wir später die Lücken dazu benutzen werden, um kleinere Teilchen hineinzusetzen. Dann wollen wir nämlich wissen, wieviele kleine Teilchen in einer Packung von 1000 großen Teilchen vorhanden sind. Die Frage soll an der kubisch dichtesten Kugelpackung in der Oktaeder- und Tetraederdarstellung geklärt werden.
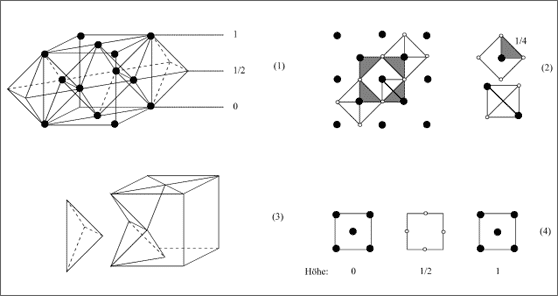
Abbildung 5.17: Anzahl von Oktaeder- und Tetraederlücken in dichtesten Kugelpackungen
Figur (1) in Abbildung 5.17 stellt als Grundkörper den flächenzentrierten Würfel dar, die Ecken und Flächenmitten des Würfels sind durch Punkte markiert. Verbindet man alle Flächenzentren miteinander, so erhält man den in den Würfel einbeschriebenen Oktaeder. An zwei anschließenden Oktaedern, die teilweise zu Nachbarwürfeln gehören, ist zu erkennen, daß deren senkrecht stehende Raumdiagonale und eine Würfelkante identisch sind.
Auf jeder Oktaederfläche des zentralen Oktaeders sitzt ein Tetraeder, von den acht Tetraedern sind übersichtshalber nur vier eingezeichnet. Die Verhältnisse, wie sie in der Draufsicht erscheinen, soll (2) darstellen. Entscheidend ist, daß die acht auf den zentralen Oktaeder aufgesetzten Tetraeder die Würfelecken liefern (vgl. auch (11) in Abb. 5.12) und zwischen diesen Ecken 1/4 eines nächsten Oktaeders seinen Platz hat. Zwei Tetraeder, zwischen die sich dieses 1/4-Oktaeder einsetzen läßt, sind in (3) veranschaulicht.
Wir können festhalten, daß hinter jeder Kante des flächenzentrierten Würfels ein Viertel-Oktaeder angeordnet ist. Die Mittelpunkte dieser Oktaeder sind mit den Kantenmitten des Würfels identisch, sie stellen die Zentren der Oktaederlücken dar. Da nun der Würfel 12 Kanten besitzt, entspricht dies 12 x 1/4 = 3 ganzen Oktaedern. Zusammen mit dem zentralen Oktaeder können wir einem kubisch flächenzentrierten Elementarwürfel vier Oktaeder zuordnen. Dieselbe Anzahl von Kugeln besitzt die Elementarzelle: 8 x 1/8 + 6 x 1/2 = 4 Vollkugeln.
Schließlich lassen sich in den betrachteten Elementarwürfel neben den vier Oktaedern acht Tetraeder einbeschreiben, das Zahlenverhältnis von Oktaedern zu Tetraedern lautet 1:2. Wenn wir also mit 1000 Kugeln eine kubisch dichteste Kugelpackung aufbauen, dann lassen sich darin 1000 Oktaeder und 2000 Tetraeder gedanklich hineinbeschreiben.
Dieselben Überlegungen an etwas komplizierteren Schnittfiguren führen bei der hexagonal dichtesten Kugelpackung zum gleichen Ergebnis: In den dichtesten Kugelpackungen lautet das Zahlenverhältnis Kugeln : Oktaeder : Tetraeder = 1 : 1 : 2.
Man kann auch formulieren: In dichtesten Kugelpackungen befinden sich ebensoviele Oktaederlücken wie Kugeln, aber doppelt soviele Tetraederlücken.
![]()


