5.1.2 Raumgittermodelle
Anhand der hexagonal dichtesten oder kubisch dichtesten Kugelpackung lassen sich viele Fragestellungen erhellen - allerdings sind die Kugelpackungen undurchsichtig, die Zuordnung von einer Kugel zur anderen im Inneren ist nicht zu sehen. Über-sichtlicher werden die Darstellungen, wenn wir alle Kugeln im gleichen Maße für ein Raumgitter auseinanderziehen oder nur die Mittelpunkte der Kugeln in den Packungen markieren. So kann man in den Gitterausschnitten der hexagonal dichtesten Ku-gelpackung die Kugelmittelpunkte durch Linien verbinden (vgl. (1) und (2) in Abb. 5.9) oder die kubisch dichteste Kugelpackung durch verschiedene Gitterzeichnungen dargestellen (vgl. (3) und (4) in Abb. 5.9).
Es ist zu beachten, daß die Auswahl verschiedener Packungsausschnitte, das Markieren der Kugelmittelpunkte durch kleine oder große Kugeln, oder die verschiedene Art und Weise, diese Kugelmittelpunkte zu verbinden, immer wieder zu anderen Bildern führt. Um einen Packungsausschnitt als Raummodell zu bauen, werden meistens Kugeln durch dicke Drähte verbunden und so an ihrem Platz gehalten: das verleiht den Modellen das Aussehen eines "Gitters".
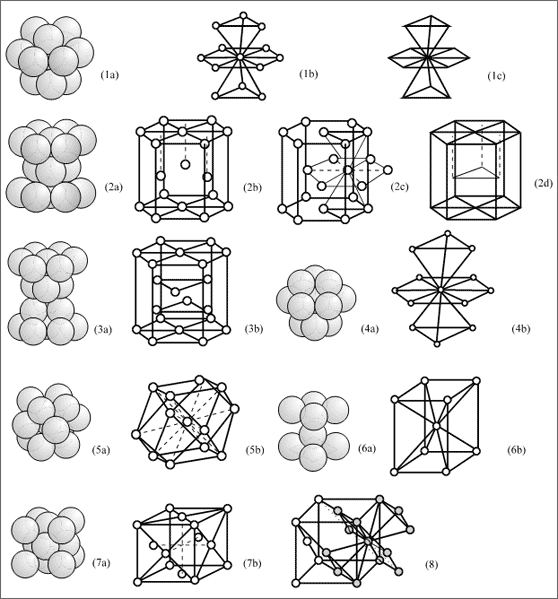
Abb. 5.9: Hexagonal und kubisch dichteste Kugelpackung in verschiedener Darstellung
Insofern haben sich aus diesen und anderen Gründen die Ausdrücke Gitter, Raum-gitter oder Kristallgitter ganz allgemein zur Information über die Anordnung der Bausteine im Raum eingebürgert. Ob man dabei nur die Punkte im Raum für die Position der Kugeln angibt oder die raumerfüllenden Kugeln selbst, ist dabei gleichgültig. Nachteilig ist bei einem Raumgittermodell, daß man die Berührungsstellen der Kugeln nicht mehr direkt sehen kann. Es bedarf einiger Übung, die Kugeln in der Vorstellung zusammenzuschieben und die Berührungsstellen zu erfassen.
Es ist besonders zu betonen, daß durch die Stäbchen oder Verbindungslinien in keinem Fall Aussagen über die Bindung zwischen den Teilchen gemacht werden, also gerade nicht etwa gerichtete Bindungskräfte gemeint sind. Die Stäbe sind lediglich Zutaten, um die Kugeln an den richtigen Positionen zu verankern, sie gehören nicht zur Modellaussage. Deshalb spricht man auch von irrelevanten Zutaten bezüglich dieser Modelle.
![]()


